��Ŀ����
6����ƽ��ֱ������ϵxOy�У�A��m��0����B��m+4��0���������߶�AB��x���Ϸ��ĵ�P�������¶��壺��45��ܡ�APB��90��ʱ���Ƶ�PΪ�߶�AB�ġ����µ㡱����1���� m=2ʱ��
���ڵ�C��3��1 ����D�� 5��3 ����E�� 2��4 ���У��߶�AB�ġ����µ㡱��D��E��
����ֱ��y=x+b�ϴ����߶�AB�ġ����µ㡱����b��ȡֵ��Χ��
��2���������������������ѡһ������
��ܰ��ʾ����������ظ��Ʒ֣�
����һ��ֱ��y=-x+14��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�AB�����С����µ㡱���ڡ�MON�ڲ���ֱ��д��m��ȡֵ��Χ��
���������G��3��-1������PΪ�߶�AB�ġ����µ㡱��ֱ��GP���߶�AB�ֳ�1��3�����֣���m=1ʱ��ֱ��д����P�ĺ������ȡֵ��Χ��
���� ��1������ͼ�����������͡���ͼ�μ����жϣ��ڵ�ֱ��y=x+b������B��6��0��ʱ��b=-6����ֱ����$\widehat{AEB}$����ʱ����$\left\{\begin{array}{l}{y=x+b}\\{��x-4��^{2}+��y-2��^{2}=8}\end{array}\right.$����ȥy�����õ�2x2+��2b-12��x+b2-4b+12=0���������=0���ɵ�b2+4b-12=0�����b=2��-6���ɴ˼����жϣ�
��2������һ����֪�������͡��Ĵ�Բ�뾶Ϊ2$\sqrt{2}$��СԲ�뾶Ϊ2�����������͡���y������ʱ��m=2$\sqrt{2}$-2�����������͡���ֱ��y=-x+14����ʱ����֪�е�Ϊ��10��4������ʱB��10��0����m=6�������Ƴ���$2\sqrt{2}-2$��m��6ʱ���߶�AB�����С����µ㡱���ڡ�MON�ڲ���
���������ͼ3�У�ֱ��PG���߶�AB���ȷ֣��ٵ�ֱ��PG����Q��2��0��ʱ��ֱ��PG�Ľ���ʽΪy=-x+2����$\left\{\begin{array}{l}{y=-x+2}\\{��x-3��^{2}{+y}^{2}=4}\end{array}\right.$���M��$\frac{5-\sqrt{7}}{2}$��$\frac{-1+\sqrt{7}}{2}$����
��$\left\{\begin{array}{l}{y=-x+2}\\{��x-3��^{2}+��y-2��^{2}=8}\end{array}\right.$�����H��$\frac{3-\sqrt{7}}{2}$��$\frac{\sqrt{7}+1}{2}$�����ɵõ�P�ĺ�����ķ�ΧΪ$\frac{{3-\sqrt{7}}}{2}$��x��$\frac{{5-\sqrt{7}}}{2}$��
�ڵ�ֱ��PG����F��4��0��ʱ��ͬ������
��� �⣺��1������ͼ1�У��۲�ͼ���֪���߶�AB�ġ����µ㡱��D��E��
�ʴ�ΪD��E��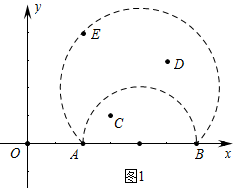
����ͼ2�У�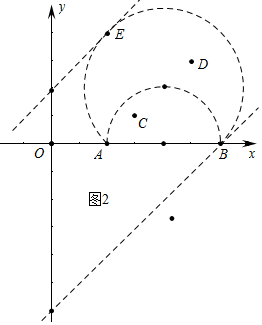
�ٵ�ֱ��y=x+b������B��6��0��ʱ��b=-6��
�ڵ�ֱ����$\widehat{AEB}$����ʱ����$\left\{\begin{array}{l}{y=x+b}\\{��x-4��^{2}+��y-2��^{2}=8}\end{array}\right.$����ȥy�����õ�2x2+��2b-12��x+b2-4b+12=0��
�������=0���ɵ�b2+4b-12=0�����b=2��-6��
������������ֱ��y=x+b�ϴ����߶�AB�ġ����µ㡱��b��ȡֵ��ΧΪ-6��b��2��
-6��b��2��
��3������1����֪�������͡��Ĵ�Բ�뾶Ϊ2$\sqrt{2}$��СԲ�뾶Ϊ2��
���������͡���y������ʱ��m=2$\sqrt{2}$-2��
���������͡���ֱ��y=-x+14����ʱ����֪�е�Ϊ��10��4������ʱB��10��0����m=6��
�൱$2\sqrt{2}-2$��m��6ʱ���߶�AB�����С����µ㡱���ڡ�MON�ڲ���
����2����ͼ3�У�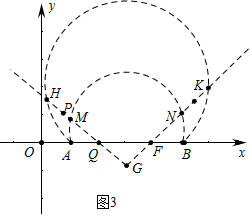
��ֱ��PG���߶�AB���ȷ֣�
�ٵ�ֱ��PG����Q��2��0��ʱ��
ֱ��PG�Ľ���ʽΪy=-x+2��
��$\left\{\begin{array}{l}{y=-x+2}\\{��x-3��^{2}{+y}^{2}=4}\end{array}\right.$���M��$\frac{5-\sqrt{7}}{2}$��$\frac{-1+\sqrt{7}}{2}$����
��$\left\{\begin{array}{l}{y=-x+2}\\{��x-3��^{2}+��y-2��^{2}=8}\end{array}\right.$�����H��$\frac{3-\sqrt{7}}{2}$��$\frac{\sqrt{7}+1}{2}$����
���P�ĺ�����ķ�ΧΪ$\frac{{3-\sqrt{7}}}{2}$��x��$\frac{{5-\sqrt{7}}}{2}$��
�ڵ�ֱ��PG����F��4��0��ʱ��
ֱ��PG�Ľ���ʽΪy=-x-4��ͬ���ɵõ�P�ĺ������ȡֵ��ΧΪ$\frac{{7+\sqrt{7}}}{2}$��x��$\frac{{9+\sqrt{7}}}{2}$��
�������������������ĵ�P�ĺ������ȡֵ��ΧΪ$\frac{{7+\sqrt{7}}}{2}$��x��$\frac{{9+\sqrt{7}}}{2}$��$\frac{{3-\sqrt{7}}}{2}$��x��$\frac{{5-\sqrt{7}}}{2}$��
���� ���⿼��һ�κ����ۺ��⡢Բ��һԪ���η����顢�����б�ʽ��֪ʶ������Ĺؼ���ѧ�����ø���Բ������⣬ѧ����ת����˼��˼�����⣬ѧ���÷��������йؽ������⣬�����п�ѹ���⣮

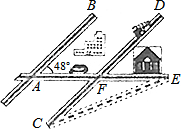 ij���м�����·��λ�ù�ϵ��ͼ��ʾ����֪AB��CD��AE��AB�ļн�Ϊ48�㣬��CF��EF�ij�����ȣ����C�Ķ���Ϊ��������
ij���м�����·��λ�ù�ϵ��ͼ��ʾ����֪AB��CD��AE��AB�ļн�Ϊ48�㣬��CF��EF�ij�����ȣ����C�Ķ���Ϊ��������| A�� | 48�� | B�� | 40�� | C�� | 30�� | D�� | 24�� |
| A�� | �����������������ߵĽ��� | B�� | �������������ϸ��ߵĽ��� | ||
| C�� | �����������ߴ�ֱƽ���ߵĽ��� | D�� | �����������ڽ�ƽ���ߵĽ��� |
��������ε�ÿ���߶���ȣ� ��������ζ�����Գ�ͼ�Σ�
��������ε���Ǻ���360�㣻��������ζ������ĶԳ�ͼ�Σ�
������ȷ�������ǣ�������
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �ڢۢ� | D�� | �٢ڢۢ� |
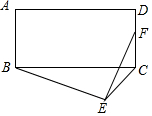 ��ͼ���ھ���ABCD�У�AB=5��AD=12����BCΪб���ھ����ⲿ��ֱ��������BEC��FΪCD���е㣬��EF�����ֵΪ��������
��ͼ���ھ���ABCD�У�AB=5��AD=12����BCΪб���ھ����ⲿ��ֱ��������BEC��FΪCD���е㣬��EF�����ֵΪ��������| A�� | $\frac{\sqrt{433}}{2}$ | B�� | $\frac{25}{4}$ | C�� | $\frac{25}{2}$ | D�� | $\frac{\sqrt{433}}{4}$ |