题目内容
8.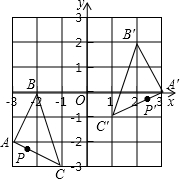 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )| A. | (-m,n+2) | B. | (-m,n-2) | C. | (-m-2,-n) | D. | (-m-2,n-2) |
分析 根据已知三对对应点的坐标,得出变换规律,再让点P的坐标也做相应变化即可.
解答 解:∵A(-3,-2),B(-2,0),C(-1,-3),
A′(3,0),B′(2,2),C′(1,-1),
∴横坐标互为相反数;纵坐标增加了0-(-2)=2-0=-1-(-3)=2;
∵B′C′边上一点P′的坐标为(m,n),
∴点P′变换前的对应点P的坐标为(-m,n-2).
故选B.
点评 本题考查了坐标与图形变化,解决本题的关键是根据已知对应点找到各对应点之间的变化规律.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
16.点A(1,y1)、B(3,y2)是反比例函数y=$\frac{9}{x}$图象上的两点,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
20.输入一组数据,按下列程序进行计算(x+8)2-826,输出结果如表:
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
17.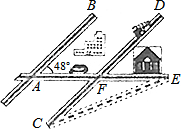 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )| A. | 48° | B. | 40° | C. | 30° | D. | 24° |
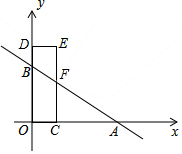 如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.
如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.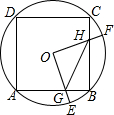 如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论: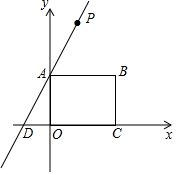 如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,以P,B,C为顶点作平行四边形PBEC,当对角线PE的值最小时,求点P的坐标.
如图,在直角坐标系中,矩形OABC的两边在坐标轴上,其中点B的坐标为(4,3),过点A的直线AD的解析式为y=2x+3,点P是直线AD上一动点,以P,B,C为顶点作平行四边形PBEC,当对角线PE的值最小时,求点P的坐标.