题目内容
14．
如图，将一长方形纸片沿EF折叠后，点DC分别落在点D′、C′的位置，若∠EFB=68°，则∠AED′=44°．
分析 先根据两直线平行，内错角相等，由AD∥BC得到∠DEF=∠EFB=68°，再利用折叠的性质得到∠D′EF=∠DEF=68°，然后利用平角的定义求解．
解答 解：∵AD∥BC，
∴∠DEF=∠EFB=68°，
∵长方形纸片沿EF折叠后，点DC分别落在点D′、C′的位置，
∴∠D′EF=∠DEF=68°，
∴∠∠AED′=180°-∠D′EF-∠DEF=180°-2×68°=44°．
故答案为44°．
点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．也考查了折叠的性质．
练习册系列答案
相关题目
4．已知3x-2y=1，用含y的代数式表示x为（ ）
| A． | x=$\frac{1+2y}{3}$ | B． | x=$\frac{1-2y}{3}$ | C． | y=$\frac{3x-1}{2}$ | D． | y=$\frac{1-3x}{2}$ |
燃灯佛舍利塔（简称燃灯塔）是通州八景之一，该塔始建于南北朝北周宇文时期，距今已有1300多年历史．燃灯塔距运河300米，是通州的象征．某同学想利用相似三角形的有关知识来求燃灯塔的高度．他先测量出燃灯塔落在地面上的影长为12米，然后在同一时刻立一根高2米的标杆，测得标杆影长为0.5米，那么燃灯塔高度为48m米．
9．在△ABC中，∠A、∠B、∠C的度数比为4：5：6，那么△ABC是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 等腰三角形 |
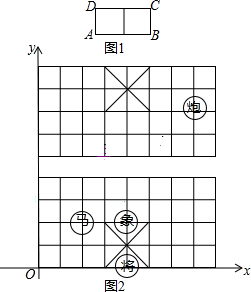中国象棋中历来有“马”走“日”，“象”飞“田”之说，其意思是：在象棋棋盘上，“马”的走法如下：以“马”所在的位置为棋格所组成的任一“日”字的一个顶点，下一步“马”可以走到该“日”字与原位置相对的那个顶点，如图1马可以自A走到C（或自C走到A）也可自B走到D（或D走到B），在如图棋盘中，建立如图2所示直角坐标系：
3．为得到二次函数y=-x2的图象，需将y=-x2+2x-2的图象（ ）
| A． | 向左平移2个单位，再向下平移2个单位 | |
| B． | 向右平移2个单位，再向上平移2个单位 | |
| C． | 向左平移1个单位，再向上平移1个单位 | |
| D． | 向右平移1个单位，再向下平移1个单位 |