题目内容
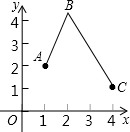 如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.
如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.(1)试问在公路边是否存在一点D,使送货路线最短?若存在,请画出D点所在的位置;
(2)若∠ADO=45°,试求出(1)中点D的坐标.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)因为AB、BC间的距离不变,所以DA、DC间的距离最小时,送货路线最短,作C关于x轴的对称点C′,连接AC′,根据轴对称确定最短路线问题,AC′与x轴的交点即为所求的点D;
(2)根据等腰直角三角形的性质求出OD的长,然后写出点D的坐标即可.
(2)根据等腰直角三角形的性质求出OD的长,然后写出点D的坐标即可.
解答: 解:(1)存在点D如图所示:
解:(1)存在点D如图所示:
(2)∵A(1,2),∠ADO=45°,
∴OD=1+2=3,
∴点D的坐标为(3,0).
 解:(1)存在点D如图所示:
解:(1)存在点D如图所示:(2)∵A(1,2),∠ADO=45°,
∴OD=1+2=3,
∴点D的坐标为(3,0).
点评:本题考查的是最短路线问题,坐标与图形性质,根据x轴上点的坐标特点求出D点的坐标即可.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列各命题的逆命题成立的是( )
| A、如果两个角都是45°,那么这两个角相等 |
| B、全等三角形的对应角相等 |
| C、两直线平行,同位角相等 |
| D、如果两个数相等,那么它们的绝对值相等 |
 如图,PA、PB为⊙O的两条切线,切点分别为A、B,直线CD切⊙O于点E.
如图,PA、PB为⊙O的两条切线,切点分别为A、B,直线CD切⊙O于点E. 如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.写出点O到△ABC的三个顶点A、B、C的距离的关系,并证明.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.写出点O到△ABC的三个顶点A、B、C的距离的关系,并证明. 如图,AD⊥BC于D,若AB+BD=DC,那么∠B与∠C有何数量关系?说明理由.
如图,AD⊥BC于D,若AB+BD=DC,那么∠B与∠C有何数量关系?说明理由. 如图,写出三个能推出直线AB∥CD的条件同时要写出它们的理由.注意:这三个条件分别要用不同的理由.
如图,写出三个能推出直线AB∥CD的条件同时要写出它们的理由.注意:这三个条件分别要用不同的理由.