题目内容
 如图,AD⊥BC于D,若AB+BD=DC,那么∠B与∠C有何数量关系?说明理由.
如图,AD⊥BC于D,若AB+BD=DC,那么∠B与∠C有何数量关系?说明理由.考点:等腰三角形的判定与性质
专题:
分析:在DC上截取DE=BD,连接AE,求出AB=CE,AB=AE,推出∠B=∠AEB,AE=EC,求出∠C=∠CAE,根据三角形外角性质求出∠AEB=2∠C,即可得出答案.
解答: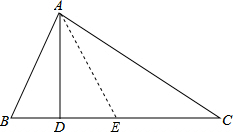 解:∠B=2∠C,
解:∠B=2∠C,
理由是:在DC上截取DE=BD,连接AE,
∵AB+BD=DC,
∴AB=CE,
∵DB=DE,AD⊥BC,
∴AB=AE,
∴∠B=∠AEB,AE=EC,
∴∠C=∠CAE,
∵∠AEB=∠C+∠CAE,
∴∠AEB=2∠C,
∴∠B=2∠C.
 解:∠B=2∠C,
解:∠B=2∠C,理由是:在DC上截取DE=BD,连接AE,
∵AB+BD=DC,
∴AB=CE,
∵DB=DE,AD⊥BC,
∴AB=AE,
∴∠B=∠AEB,AE=EC,
∴∠C=∠CAE,
∵∠AEB=∠C+∠CAE,
∴∠AEB=2∠C,
∴∠B=2∠C.
点评:本题考查了等腰三角形的性质和判定,线段垂直平分线性质,三角形外角性质的应用,解此题的关键是能正确作辅助线,题目比较好,难度适中.

练习册系列答案
相关题目
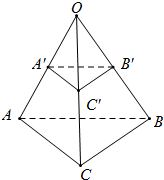 如图所示,不共面的三条直线交于O点,在O点的同侧上分别取点A和A′,B和B′,C和C′,使得
如图所示,不共面的三条直线交于O点,在O点的同侧上分别取点A和A′,B和B′,C和C′,使得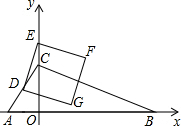 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=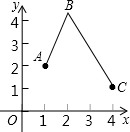 如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.
如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D. 如图所示,E为△ABC内一点,BE的延长线交AC于点D,∠1=(4m-1)°,∠2=(3m+2)°,∠A=(4m-5)°,求m的取值范围.
如图所示,E为△ABC内一点,BE的延长线交AC于点D,∠1=(4m-1)°,∠2=(3m+2)°,∠A=(4m-5)°,求m的取值范围.