题目内容
 如图,PA、PB为⊙O的两条切线,切点分别为A、B,直线CD切⊙O于点E.
如图,PA、PB为⊙O的两条切线,切点分别为A、B,直线CD切⊙O于点E.(1)试探究△PCD的周长与线段PA的数量关系;
(2)若∠P=α°,求∠COD的度数.
考点:切线的性质
专题:
分析:(1)根据切线长定理,即可得到PA=PB,ED=AD,CE=BC,从而求得三角形的周长=2PA;
(2)连接OA、OE、OB根据切线性质,∠P+∠AOB=180°,再根据CD为切线可知∠COD=
∠AOB.
(2)连接OA、OE、OB根据切线性质,∠P+∠AOB=180°,再根据CD为切线可知∠COD=
| 1 |
| 2 |
解答:解:(1)△PCD的周长=2PA.理由如下:
∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA;

(2)如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
∠AOB,
∵∠APB=α°,
∴∠AOB=180°-α°,
∴∠COD=90°-
α°.
∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=10,ED=AD,CE=BC;
∴△PCD的周长=PD+DE+PC+CE=2PA,即△PCD的周长=2PA;

(2)如图,连接OA、OE、OB.
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
| 1 |
| 2 |
∵∠APB=α°,
∴∠AOB=180°-α°,
∴∠COD=90°-
| 1 |
| 2 |
点评:本题考查了切线的性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题,是基础题型.

练习册系列答案
相关题目
 由若干块形状相同的小正方块搭成的立体模型的主视图与俯视图如下,则不同的搭法总数为( )
由若干块形状相同的小正方块搭成的立体模型的主视图与俯视图如下,则不同的搭法总数为( )| A、1 | B、2 | C、3 | D、4 |
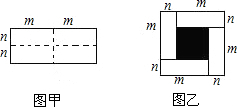 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.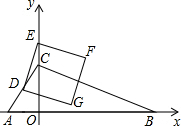 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=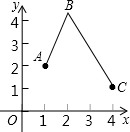 如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.
如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D. 如图所示,E为△ABC内一点,BE的延长线交AC于点D,∠1=(4m-1)°,∠2=(3m+2)°,∠A=(4m-5)°,求m的取值范围.
如图所示,E为△ABC内一点,BE的延长线交AC于点D,∠1=(4m-1)°,∠2=(3m+2)°,∠A=(4m-5)°,求m的取值范围.