题目内容
 如图,直线AB,CD相交于O,OE平分∠AOD,FO⊥CD于点O,∠1=
如图,直线AB,CD相交于O,OE平分∠AOD,FO⊥CD于点O,∠1=| 4 |
| 5 |
考点:对顶角、邻补角,角平分线的定义,垂线
专题:
分析:根据对顶角的性质,可得∠2与∠3的关系,根据垂直的定义,可得∠DOF的度数,根据角的和差,可得∠1、∠3的度数,根据角的和差,可得∠COB的度数,根据对顶角的性质,可得∠AOD的度数,根据角平分线的性质,可得∠4的大小,根据角的和差,可得答案.
解答:解:由对顶角相等得∠3=∠2,
∠1=
∠2,
∠1=
∠3
由FO⊥CD于点O,
∠FOD=90°,
∠1+∠3=∠FOD=90°,
∠3+
∠3=90°
∠3=50°∠1=30°,
∠AOD=∠BOC=∠1+∠COF=30°+90°=120°,
OE平分∠AOD,
∴∠4=
∠AOD=60°,
∠EOF=∠4+∠DOF=60°+90°=150°.
∠1=
| 4 |
| 5 |
∠1=
| 4 |
| 5 |
由FO⊥CD于点O,
∠FOD=90°,
∠1+∠3=∠FOD=90°,
∠3+
| 4 |
| 5 |
∠3=50°∠1=30°,
∠AOD=∠BOC=∠1+∠COF=30°+90°=120°,
OE平分∠AOD,
∴∠4=
| 1 |
| 2 |
∠EOF=∠4+∠DOF=60°+90°=150°.
点评:本题考查了对顶角与邻补角,利用了对顶角相等,垂直的定义,角平分线的性质,角的和差.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目

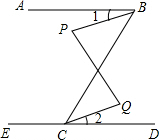 如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.
如图,已知∠ABC=63°,∠ECB=117°,∠P=∠Q.