题目内容
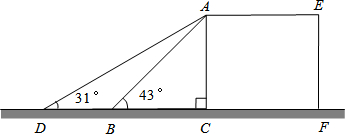
某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为43°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD是改造后的斜坡(D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)
[参考数据:sin43°=0.682,cos43°=0.731,tan43°=0.933;sin31°=0.515,cos31°=0.857,tan31°=0.601].
[参考数据:sin43°=0.682,cos43°=0.731,tan43°=0.933;sin31°=0.515,cos31°=0.857,tan31°=0.601].

考点:解直角三角形的应用-坡度坡角问题
专题:
分析:首先根据∠ABC=43°,AB=2m,在Rt△ABC中,求出AC的长度,然后根据∠ADC=31°,利用三角函数的知识在Rt△ACD中求出CD的长度.
解答:解:在Rt△ABC中,
∵∠ABC=43°,AB=2m,
∴AC=AB•sin43°=2×0.682=1.364 (m)
在Rt△ADC中,
∵∠ADC=31°,
∴CD=
=
≈2.27(m).
即斜坡AD底端D与平台AC的距离CD为2.27m.
∵∠ABC=43°,AB=2m,
∴AC=AB•sin43°=2×0.682=1.364 (m)
在Rt△ADC中,
∵∠ADC=31°,
∴CD=
| AC |
| tan31° |
| 1.364 |
| 0.601 |
即斜坡AD底端D与平台AC的距离CD为2.27m.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造之间三角形,利用三角函数的知识解直角三角形.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,
如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD, 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图,直线AB,CD相交于O,OE平分∠AOD,FO⊥CD于点O,∠1=
如图,直线AB,CD相交于O,OE平分∠AOD,FO⊥CD于点O,∠1=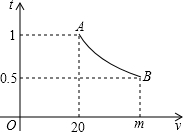 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=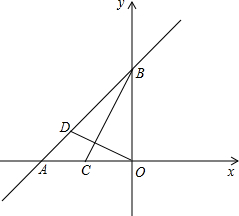 如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点B,点C(-2,0).
如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点B,点C(-2,0).