题目内容
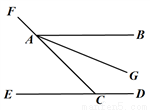
19. 甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
分析 根据题意得出AC,AB的长,再利用勾股定理的逆定理得出△BAC是直角三角形,进而得出答案.
解答 解:由题意可得:
AC=15×4=60(海里),
AB=20×4=80(海里),
AC2+AB2=602+802=10000,
BC2=10000,
故AC2+AB2=BC2,
∴△BAC是直角三角形,
∴∠BAC=90°,
180°-40°-90°=50°,
∴乙船航行的方向是南偏东50°(或东偏南40°).
点评 此题主要考查了勾股定理的应用,根据题意得出△BAC是直角三角形是解题关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
12.现有一个正八边形的纸片,则该纸片每个内角的外角的度数为( )
| A. | 60° | B. | 50° | C. | 45° | D. | 30° |