题目内容
1.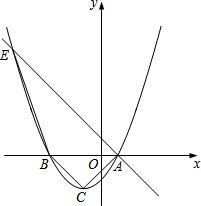 如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.
如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.(1)求m的值和抛物线的解析式;
(2)已知过点A的直线y=-x+1交抛物线于另一点E.若点P在x轴上,以点P、B、C为顶点的三角形与△AEB相似,求点P的坐标;
(3)在(2)的条件下,△BCP的外接圆半径等于$\frac{\sqrt{26}}{2}$或$\frac{2\sqrt{13}}{5}$.(直接写答案)
分析 (1)由二次函数图象的对称性、对称轴及A点坐标,可求出m值,利用直角三角形可以求出C点坐标,利用交点式和C点坐标,求出二次函数解析式;
(2)联立直线AE和二次函数的解析式即可求得E点的坐标,此时可发现∠ABE=45°,若以P、B、C为顶点的三角形与△ABE相似,可考虑两种情况:①△BCP∽△AEB,②△BCP∽△ABE;根据上述两种情况所得到的不同比例线段即可求出BP的长,从而确定P点的坐标.
(3)根据三角形外接圆性质,可知.外接圆心在三角形三边垂直平分线上,因此只需求出三角形两边垂直平分线的直线解析式,联立方程组,即可求出三角形外接圆圆心,然后利用两点之间距离公式,即可求出三角形外接圆半径.
解答 解:(1)∵抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,
∴点B的坐标为(m,0),
即m=-3,
∵∠ACB=90°,AC=BC,
∴点C的坐标为(-1,-2),
设抛物线的解析式为y=a(x-1)(x+3),
将点C(-1.-2)代入,
则a=$\frac{1}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$x2+x-$\frac{3}{2}$;
(2)联立直线AE与二次函数解析式得:
$\left\{\begin{array}{l}{y=-x+1}\\{y=\frac{1}{2}{x}^{2}+x-\frac{3}{2}}\end{array}\right.$
解得:x1=1,x2=-5
∴E(-5,6)
∴AE=6$\sqrt{2}$,AB=4,BC=2$\sqrt{2}$,
∵∠BAE=∠BCP=45°
∴△BCP与△ABE相似分为以下两种情况:
①当△BCP∽△ABE时得:
$\frac{AB}{BC}=\frac{AE}{BP}$,
∴$\frac{4}{2\sqrt{2}}=\frac{6\sqrt{2}}{BP}$
∴BP=6
P(3,0)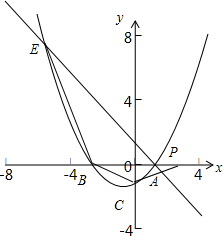
②当△BCP∽△AEB时得:
$\frac{AB}{BP}=\frac{AE}{BC}$
∴$\frac{4}{BP}=\frac{6\sqrt{2}}{2\sqrt{2}}$
∴BP=$\frac{4}{3}$
∴P(-$\frac{5}{3}$,0)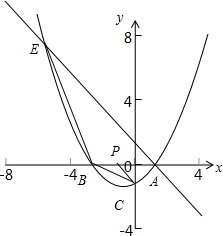
综上所述:P(3,0)或P(-$\frac{5}{3}$,0).
(3)当点P(3,0)时
线段BP的垂直平分线为x=0
线段BC的垂直平分线为y=x+1
联立方程组:$\left\{\begin{array}{l}{x=0}\\{y=x+1}\end{array}\right.$
解得圆心坐标为(0,1)
∴外接圆半径为$\sqrt{(0+3)^{2}+(1-0)^{2}}$=$\sqrt{10}$
同理:当点P坐标为(-$\frac{5}{3}$,0)
线段BP的垂直平分线为x=-$\frac{7}{3}$
线段BC的垂直平分线为y=x+1
联立方程组:$\left\{\begin{array}{l}{x=-\frac{7}{3}}\\{y=x+1}\end{array}\right.$
解得圆心坐标为(-$\frac{7}{3}$,-$\frac{5}{3}$)
∴外接圆半径为$\frac{\sqrt{29}}{3}$
综上所述:外接圆半径为$\sqrt{10}$或$\frac{\sqrt{29}}{3}$.
点评 本题目很好地将二次函数、三角形相似、圆知识点很好地结合,既考查了学生的知识点宽度,也考察学生知识掌握的深度,是很不错的题目.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案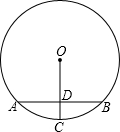 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
 如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
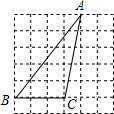 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠B的值为$\frac{5}{4}$.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠B的值为$\frac{5}{4}$.