题目内容
已知在⊙O中,半径r=13,弦AB∥CD,且AB=24,CD=10,则AB与CD的距离为( )
| A、5 | B、7 | C、17 | D、7或17 |
考点:垂径定理,勾股定理
专题:分类讨论
分析:过O作OE⊥AB交AB于E点,过O作OF⊥CD交CD于F点,连接OA、OC,由题意可得:OA=OC=13,AE=EB=12,CF=FD=5,E、F、O在一条直线上,EF为AB、CD之间的距离,再分别解Rt△OEA、Rt△OFC,即可得OE、OF的长,然后分AB、CD在圆心的同侧和异侧两种情况求得AB与CD的距离.
解答: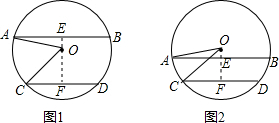 解:①当AB、CD在圆心两侧时;
解:①当AB、CD在圆心两侧时;
过O作OE⊥AB交AB于E点,过O作OF⊥CD交CD于F点,连接OA、OC,如图1所示:
∵半径r=13,弦AB∥CD,且AB=24,CD=10
∴OA=OC=13,AE=EB=12,CF=FD=5,E、F、O在一条直线上
∴EF为AB、CD之间的距离
在Rt△OEA中,由勾股定理可得:
OE2=OA2-AE2
∴OE=
=5
在Rt△OFC中,由勾股定理可得:
OF2=OC2-CF2
∴OF=
=12
∴EF=OE+OF=17
AB与CD的距离为17;
②当AB、CD在圆心同侧时,如图2所示:
同①可得:OE=5,OF=12;
则AB与CD的距离为:OF-OE=7;
综上所述,AB与C D间的距离是17或7.
故选:D.
 解:①当AB、CD在圆心两侧时;
解:①当AB、CD在圆心两侧时;过O作OE⊥AB交AB于E点,过O作OF⊥CD交CD于F点,连接OA、OC,如图1所示:
∵半径r=13,弦AB∥CD,且AB=24,CD=10
∴OA=OC=13,AE=EB=12,CF=FD=5,E、F、O在一条直线上
∴EF为AB、CD之间的距离
在Rt△OEA中,由勾股定理可得:
OE2=OA2-AE2
∴OE=
| 132-122 |
在Rt△OFC中,由勾股定理可得:
OF2=OC2-CF2
∴OF=
| 132-52 |
∴EF=OE+OF=17
AB与CD的距离为17;
②当AB、CD在圆心同侧时,如图2所示:
同①可得:OE=5,OF=12;
则AB与CD的距离为:OF-OE=7;
综上所述,AB与C D间的距离是17或7.
故选:D.
点评:本题考查了垂径定理以及解直角三角形的运用.解题时,需要分类讨论,以防漏解.

练习册系列答案
相关题目
若一元二次方程(m-1)x2+(m2+1)x+m2-1=0的常数项为0,则m的值为( )
| A、1 | B、-1 | C、±1 | D、0 |
 如图,在正方形ABCD中,F是AD边的中点,E是BA延长线上一点,且AE=
如图,在正方形ABCD中,F是AD边的中点,E是BA延长线上一点,且AE=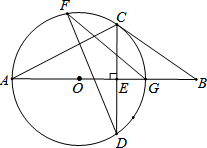 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.



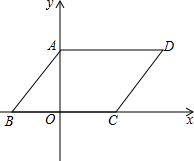 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.