题目内容
19. 如图,已知∠1=36°,∠2=36°,∠3=140°,则∠4的度数等于( )
如图,已知∠1=36°,∠2=36°,∠3=140°,则∠4的度数等于( )| A. | 40° | B. | 36° | C. | 44° | D. | 100° |
分析 根据平行线的性质和判定定理即可得到结论.
解答 解:∵∠1=36°,∠2=36°,
∴∠1=∠2,
∴PQ∥MN,
∴∠4=PNM=180°-∠3=40°,
故选A.
点评 本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
9.根据方程x2-3x-5=0可列表如下( )
则x的取值范围是( )
| x | -3 | -2 | -1 | … | 4 | 5 | 6 |
| x2-3x-5 | 13 | 5 | -1 | … | -1 | 5 | 13 |
| A. | -1<x<4 | B. | -2<x<-1 | C. | 4<x<5 | D. | -2<x<-1或4<x<5 |
10.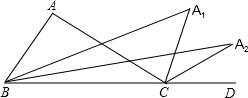 如图,△ABC中,∠A=α°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠An-1BC与∠An-1CD的平分线相交于点An,则∠An的度数为( )
如图,△ABC中,∠A=α°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠An-1BC与∠An-1CD的平分线相交于点An,则∠An的度数为( )
 如图,△ABC中,∠A=α°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠An-1BC与∠An-1CD的平分线相交于点An,则∠An的度数为( )
如图,△ABC中,∠A=α°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠An-1BC与∠An-1CD的平分线相交于点An,则∠An的度数为( )| A. | ${({\frac{α}{n}})°}$ | B. | ${({\frac{α}{2n}})°}$ | C. | ${({\frac{α}{2^n}})°}$ | D. | ${({\frac{α}{{{2^{n+1}}}}})°}$ |
7. 如图,在△ABC中,∠ACB=90°,CD为∠ACB的平分线,过点D作DE⊥BC于E,DF⊥AC于F,若AF=8,BE=6,则CE的长为( )
如图,在△ABC中,∠ACB=90°,CD为∠ACB的平分线,过点D作DE⊥BC于E,DF⊥AC于F,若AF=8,BE=6,则CE的长为( )
 如图,在△ABC中,∠ACB=90°,CD为∠ACB的平分线,过点D作DE⊥BC于E,DF⊥AC于F,若AF=8,BE=6,则CE的长为( )
如图,在△ABC中,∠ACB=90°,CD为∠ACB的平分线,过点D作DE⊥BC于E,DF⊥AC于F,若AF=8,BE=6,则CE的长为( )| A. | 8 | B. | $4\sqrt{3}$ | C. | 7 | D. | 6 |
4.如果-x×(-4)=$\frac{8}{5}$,则x的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
12. 如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
 如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )| A. | 3,3,3 | B. | 1,2,3 | C. | 1,3,6 | D. | 3,2,6 |
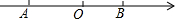 如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0.
如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0. 如图是某公司今年1到4月份的总产值相对上个月的增长率统计图,下列说法:
如图是某公司今年1到4月份的总产值相对上个月的增长率统计图,下列说法: