题目内容
4.如图1,在等边△ABC中,点P以每秒1厘米的速度从点A出发,沿折线AB-BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )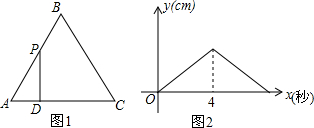
| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\frac{5\sqrt{3}}{4}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 由题意和等边三角形的性质得出AB=BC=4,∠C=60°,再由三角函数即可求出PD的长.
解答 解:根据题意得:AB=4,
∵△ABC是等边三角形,
∴AB=BC=4,∠C=60°, 当点P运动5.5秒时,如图所示:
当点P运动5.5秒时,如图所示:
则BP=5.5-4=1.5,
∴PC=2.5,
∴PD=PC•sin60°=2.5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$;
故选:B.
点评 本题考查了动点问题的函数图象、等边三角形的性质、三角函数的运用;熟练掌握等边三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
7.估计$\frac{\sqrt{5}-1}{2}$介于( )
| A. | 0.4与0.5之间 | B. | 0.5与0.6之间 | C. | 0.6与0.7之间 | D. | 0.7与0.8之间 |
15.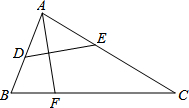 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
12. 如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
 如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )| A. | 30°或50° | B. | 30°或60° | C. | 40°或50° | D. | 40°或60° |
19.某服装经销商发现某款新型运动服市场需求量较大,经过市场调查发现年销售量y(件)与销售单价x(元)之间存在如图1所示的一次函数关系,而该服装的进价z(元)与销售量y(件)之间的关系如下表所示.已知每年支付员工工资和场地租金等费用总计2万元.
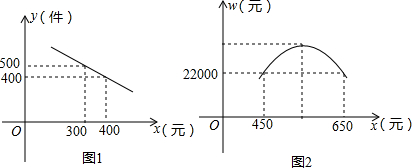
(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
| 销售数量y(件) | … | 300 | 400 | 500 | 600 | … |
| 进货价格z(元) | … | 340 | 320 | 300 | 280 | … |

(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
13.下面每个表格中的四个数都是按相同规律填写的:
根据此规律确定x的值为( )

根据此规律确定x的值为( )
| A. | 135 | B. | 170 | C. | 209 | D. | 252 |
14.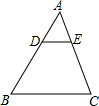 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
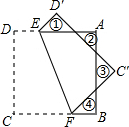 如图,将正方形纸片ABCD沿直线EF折叠,若图中①、②、③、④四个三角形的周长之和为8,则正方形ABCD的面积为4.
如图,将正方形纸片ABCD沿直线EF折叠,若图中①、②、③、④四个三角形的周长之和为8,则正方形ABCD的面积为4.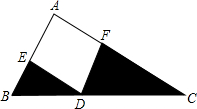 如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.
如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.