题目内容
分别写出下列函数的图象的开口方向、对称轴、顶点坐标.
(1)y=3x2-2
(2)y=4(x-1)2
(3)y=x2+x
(4)y=x(4-x)-6.
(1)y=3x2-2
(2)y=4(x-1)2
(3)y=x2+x
(4)y=x(4-x)-6.
考点:二次函数的性质
专题:
分析:结合二次函数的解析,把其化为顶点式则可得出其开口方程、对称轴和顶点坐标.
解答:解:
(1)∵y=3x2-2,
∴二次函数的图象开口向上,对称轴为x=0,顶点坐标为(0,-2);
(2)∵y=4(x-1)2,
∴二次函数的图象开口向上,对称轴为x=1,顶点坐标为(1,0);
(3)y=x2+x=(x+
)2-
∴二次函数的图象开口向上,对称轴为x=-
,顶点坐标为(-
,-
);
(4)y=x(4-x)-6=-x2+4x-6=-(x-2)2-10,
∴二次函数的图象开口向下,对称轴为x=2,顶点坐标为(2,-10).
(1)∵y=3x2-2,
∴二次函数的图象开口向上,对称轴为x=0,顶点坐标为(0,-2);
(2)∵y=4(x-1)2,
∴二次函数的图象开口向上,对称轴为x=1,顶点坐标为(1,0);
(3)y=x2+x=(x+
| 1 |
| 2 |
| 1 |
| 4 |
∴二次函数的图象开口向上,对称轴为x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(4)y=x(4-x)-6=-x2+4x-6=-(x-2)2-10,
∴二次函数的图象开口向下,对称轴为x=2,顶点坐标为(2,-10).
点评:本题主要考查二次函数的开口方向、对称轴方程及顶点坐标,掌握二次函数的顶点式y=a(x-h)2+k是解题的关键.

练习册系列答案
相关题目
等腰三角形的两边分别为5和8,那么它的周长是( )
| A、13 | B、18 |
| C、21 | D、18或21 |
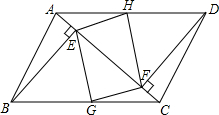 如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.
如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远. 如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.
如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.