题目内容
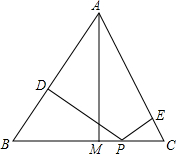 如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h,请探究图中的h1、h2、h3、h的关系.
如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h,请探究图中的h1、h2、h3、h的关系.考点:等边三角形的性质
专题:
分析:把点P与各顶点分别连接起来.根据组合图形的面积与分割成的图形面积之间的关系建立关系式,然后根据等边三角形性质求解;分三种情况讨论;
解答:解:
当点P在BC边上时,如图(1),
连接AP,则 S△ABC=S△ABP+S△APC
∴
BC•AM=
AB•PD+
AC•PF
即
BC•h=
AB•h1+
AC•h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2.
当点P在△ABC内,如图(2),
连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴
BC•AM=
AB•PD+
AC•PF+
BC•PE
即
BC•h=
AB•h1+
AC•h2+
BC•h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3.
当点P在△ABC外时,如图(3).
连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC-S△PBC,
即
BC•AM=
AB•PD+
AC•PE-
BC•PF,
∵AB=BC=AC,
∴h1+h2-h3=h,
即h1+h2-h3=h.

当点P在BC边上时,如图(1),
连接AP,则 S△ABC=S△ABP+S△APC
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2.
当点P在△ABC内,如图(2),
连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3.
当点P在△ABC外时,如图(3).
连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC-S△PBC,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC=AC,
∴h1+h2-h3=h,
即h1+h2-h3=h.
点评:此题考查等边三角形的性质,运用等积法建立关系构思巧妙,也是此题的难点.

练习册系列答案
相关题目
 如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为
如图所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为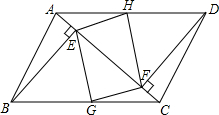 如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.
如图是某市一公园的路面示意图,其中四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,E、F是垂足,G、H分别是BC、AD的中点,连接EG、GF、FH、HE为公园中小路.问小明从B地经E地、H地到F地与小强从D地经F地、G地到E地,谁的路程远.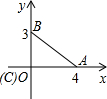 以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为
以直角三角形的直角顶点C为坐标原点,以CA所在直线为x轴,建立直角坐标系,如图所示,则Rt△ABC的周长为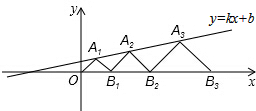 在平面直角坐标系xOy中,点A1,A2,A3…和B1,B2,B3…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系xOy中,点A1,A2,A3…和B1,B2,B3…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2( 如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.
如图,P是半径为2的⊙O外一点,PB是⊙O的切线,B为切点,弦BC∥OA,且BC=2,求图中阴影部分面积.