题目内容
如图，在△ABC中，CF：EF：BE=3：2：1，BD：AD=2：3．求CH：HG：DG的比．考点：平行线分线段成比例
专题：计算题
分析：作DM∥AE于M，DN∥AF于N，如图，根据平行线分线段成比例，由DM∥AE得到
=
=
，于是设BM=2x，则ME=3x，BE=5x，于是得到CF=15x，EF=10x，
再由GE∥DM得到
=
=
，于是设DG=3t，则DC=28t，接着利用DN∥AF得到
=
=
，则可计算出NF=9x，然后利用HF∥DN得到
=
，可计算出DH=
t，再分别计算出GH=DH-DG=
t，CH=CD-DH=
t，最后计算CH：HG：DG的值．
| BM |
| ME |
| BD |
| DA |
| 2 |
| 3 |
再由GE∥DM得到
| DG |
| DC |
| ME |
| MC |
| 3 |
| 28 |
| BN |
| NF |
| BD |
| DA |
| 2 |
| 3 |
| DH |
| DC |
| NF |
| NC |
| 21 |
| 2 |
| 15 |
| 2 |
| 35 |
| 2 |
解答：解：作DM∥AE于M，DN∥AF于N，如图，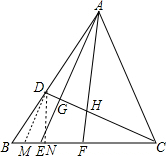
∵DM∥AE，
∴
=
=
，
设BM=2x，则ME=3x，BE=5x，
∵CF：EF：BE=3：2：1，
∴CF=15x，EF=10x，
∵GE∥DM，
∴
=
=
=
，
设DG=3t，则DC=28t，
∵DN∥AF，
∴
=
=
，
而BN+NF=BF=15x，
∴NF=9x，
∵HF∥DN，
∴
=
，即
=
=
，
∴DH=
t，
∴GH=DH-DG=
t-3t=
t，CH=CD-DH=28t-
t=
t，
∴CH：HG：DG=
t：
t：3t=35：15：6．
∵DM∥AE，
∴
| BM |
| ME |
| BD |
| DA |
| 2 |
| 3 |
设BM=2x，则ME=3x，BE=5x，
∵CF：EF：BE=3：2：1，
∴CF=15x，EF=10x，
∵GE∥DM，
∴
| DG |
| DC |
| ME |
| MC |
| 3x |
| 3x+10x+15x |
| 3 |
| 28 |
设DG=3t，则DC=28t，
∵DN∥AF，
∴
| BN |
| NF |
| BD |
| DA |
| 2 |
| 3 |
而BN+NF=BF=15x，
∴NF=9x，
∵HF∥DN，
∴
| DH |
| DC |
| NF |
| NC |
| DH |
| 28t |
| 9x |
| 9x+15x |
| 3 |
| 8 |
∴DH=
| 21 |
| 2 |
∴GH=DH-DG=
| 21 |
| 2 |
| 15 |
| 2 |
| 21 |
| 2 |
| 35 |
| 2 |
∴CH：HG：DG=
| 35 |
| 2 |
| 15 |
| 2 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，在等腰梯形ABCD中，AD∥BC，AB=CD=AD=2cm，∠BAD=120°，P为AD的中点，在直线AD下方作∠BPE=120°，使边PE与等腰梯形的某一边所在直线相交于点E．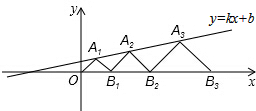
在平面直角坐标系xOy中，点A1，A2，A3…和B1，B2，B3…分别在直线y=kx+b和x轴上，△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形，如果A1（1，1），A2（
如图，P是半径为2的⊙O外一点，PB是⊙O的切线，B为切点，弦BC∥OA，且BC=2，求图中阴影部分面积．
如图，在Rt△ABC中，∠C=90°，AC=BC=a，延长CA到D，使AD=AB，连接BD．