题目内容
18.?ABCD中,∠A=45°,AD=2,AB=x,过点D作AB、BC边上的高DE、DF,记BE+BF=y.(1)请画出图形,直接写出y关于x的函数解析式以及自变量x的取值范围;
(2)当y=$1+\frac{{\sqrt{2}}}{2}$时,x=2$\sqrt{2}$+1.
分析 (1)由?ABCD中,∠A=45°,AD=2,AB=x,可求得AE与CF的长,继而求得BE+BF的长,即可求得y关于x的函数解析式,然后由平行四边形的性质,求得自变量x的取值范围;
(2)由y=$1+\frac{{\sqrt{2}}}{2}$,可得方程:1+$\frac{\sqrt{2}}{2}$=$\frac{2-\sqrt{2}}{2}$x+2-$\sqrt{2}$,继而求得答案.
解答 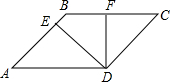 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴∠C=∠A=45°,BC=AD=2,CD=AB=x,
∵DE⊥AB,DF⊥BC,AD=2,AB=x,
∴AE=AD•cos∠A=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,CF=CD•cos∠C=$\frac{\sqrt{2}}{2}$x,
∴BE=AB-AE=x-$\sqrt{2}$,BC-CF=2-$\frac{\sqrt{2}}{2}$x,
∴y=BE+BF=x-$\sqrt{2}$+2-$\frac{\sqrt{2}}{2}$x=$\frac{2-\sqrt{2}}{2}$x+2-$\sqrt{2}$(x≥$\sqrt{2}$);
(2)当y=1+$\frac{\sqrt{2}}{2}$时,1+$\frac{\sqrt{2}}{2}$=$\frac{2-\sqrt{2}}{2}$x+2-$\sqrt{2}$,
解得:x=2$\sqrt{2}$+1.
故答案为:2$\sqrt{2}$+1.
点评 此题考查了平行四边形的性质以及等腰直角三角形性质.注意准确画出图形是关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
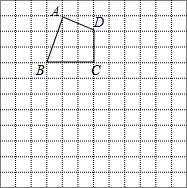 作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上)
作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上)