题目内容
4.若$\sqrt{m+3}$+(n-2)2=0,则mn=9.分析 首先根据非负数的性质:算术平方根具有非负性,以及任意一个数的偶次方都是非负数,可得$\sqrt{m+3}$=0,n-2=0,据此分别求出m、n的大小,然后根据幂的求法,求出mn的值是多少即可.
解答 解:因为$\sqrt{m+3}$+(n-2)2=0,
所以$\sqrt{m+3}$=0,n-2=0,
所以m=-3,n=2,
则mn=(-3)2=9.
故答案为:9.
点评 此题主要考查了非负数的性质:算术平方根具有非负性,以及任意一个数的偶次方都是非负数,还有幂的求法,要熟练掌握,解答此题的关键是求出m、n的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
 如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
如图,直线AB、CD被直线EF所截,则∠3的内错角是( )| A. | ∠1 | B. | ∠2 | C. | ∠4 | D. | ∠5 |
19.在下列各式中正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | ±$\sqrt{9}$=3 | C. | $\sqrt{{2}^{2}}$=2 | D. | $\sqrt{16}$=8 |
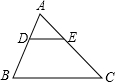 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( ) 如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.
如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由. 如图,在△ABC中,AB=AC,AD=DB=BC,DE⊥AB于点E,若CD=4,且△BDC的周长为24,求AE的长.
如图,在△ABC中,AB=AC,AD=DB=BC,DE⊥AB于点E,若CD=4,且△BDC的周长为24,求AE的长. 如图,?ABCD的对角线AC、BD相交于点0,EF过点O与AD、BC分别相交于点E、F,若AB=5,AD=8,OE=3,那么四边形EFCD的周长为19.
如图,?ABCD的对角线AC、BD相交于点0,EF过点O与AD、BC分别相交于点E、F,若AB=5,AD=8,OE=3,那么四边形EFCD的周长为19.