题目内容
8. 如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.
如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.
分析 首先作A关于CD的对称点Q,连接BQ,然后根据圆周角定理、圆的对称性质和等边三角形的性质解答.
解答  解:作A关于CD的对称点Q,连接CQ,BQ,BQ交CD于P,此时AP+PB=QP+PB=QB,
解:作A关于CD的对称点Q,连接CQ,BQ,BQ交CD于P,此时AP+PB=QP+PB=QB,
根据两点之间线段最短,PA+PB的最小值为QB的长度,
连接OQ,OB,
∵点B为弧AD 的中点,
∴∠BOD=∠ACD=20°,
∴∠QOD=2∠QCD=2×20°=40°,
∴∠BOQ=20°+40°=60°.
∵OB=OQ,
∴△BOQ是等边三角形,
BQ=OB=$\frac{1}{2}$CD=2,即PA+PB的最小值为2.
故答案为2.
点评 本题考查的是轴对称-最短路线问题,解答此题的关键是找到点A的对称点,把题目的问题转化为两点之间线段最短解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.一个几何体的主视图、左视图都是等边三角形,俯视图是一个圆,这个几何体是( )
| A. | 三棱柱 | B. | 三棱锥 | C. | 圆柱 | D. | 圆锥 |
16.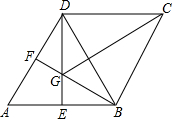 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )
 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
 如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )
如图,△ABC中,D为BC上的点,DC=2BD,以DC为直径作圆交AB于点E,若AE=AC,则sinB的值为( )| A. | $\frac{2}{5}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{10}}{8}$ | D. | $\frac{3\sqrt{6}}{8}$ |
18.2017年3月5日,李克强总理在十二届全国人大五次会议上作政府工作报告谈到,2016年我国国内生产总值达到74.4万亿元,增长6.7%,名列世界前茅.其中74.4万亿元用科学记数法表示为( )
| A. | 7.44×1013元 | B. | 7.44×1012元 | C. | 74.4×1012元 | D. | 7.44×1014元 |
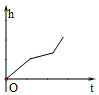
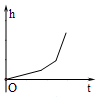
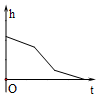
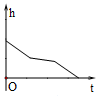
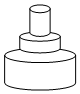 如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )
如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )