题目内容
2.某校1000名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为100人;
(2)四月日均诵读时间的统计表中的a值分别为32;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多30人;
(4)根据抽样调查结果,请你估计该校学生四月份人均诵读时间在1小时以上的人数.
分析 (1)根据统计表第一组的人数是6,所占的百分比是6%,即可求得调查的总人数;
(2)首先求得四月份1<x≤1.5组的人数是,然后利用总人数减去其它组的人数求得a的值;
(3)用四月份的人数减去三月份的人数即可求解;
(4)利用总人数1000乘以对应的比例即可求解.
解答 解:(1)调查的人数是6÷6%=100.
故答案是:100;
(2)四月份1<x≤1.5组的人数是100×52%=52(人),
则a=100-6-52-10=32,
故答案是:32;
(3)52-32=20.
故答案是30;
(4)估计该校学生四月份人均诵读时间在1小时以上的人数是1000×$\frac{10}{100}$=100(人).
点评 本题考查频数分布直方图、频数分布表、用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
相关题目
7.抛物线y=x2-2x+m2+2(m是常数)的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.在△ABC中,AB=4$\sqrt{2}$,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是6$\sqrt{2}$-6≤CD≤5.
11.有甲、乙、丙三种货物,若购甲3件、乙2件、丙1件,共需315元,若购甲1件,乙2件,丙3件共需285元,那么购甲、乙、丙各1件,共需( )
| A. | 128元 | B. | 130元 | C. | 150元 | D. | 160元 |
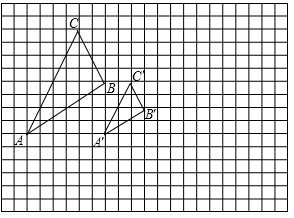 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,他们的顶点都在小正方形的顶点上.
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,他们的顶点都在小正方形的顶点上.