题目内容
7.抛物线y=x2-2x+m2+2(m是常数)的顶点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 先根据抛物线的顶点式求出抛物线y=x2-2x+m2+2(m是常数)的顶点坐标,再根据各象限内点的坐标特点进行解答.
解答 解:∵y=x2-2x+m2+2=(x-1)2+(m2+1),
∴顶点坐标为:(1,m2+1),
∵1>0,m2+1>0,
∴顶点在第一象限.
故选A.
点评 本题考查的是二次函数的性质及各象限内点的坐标特点,根据题意得出抛物线的顶点坐标是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
17.2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
15.某6人活动小组为了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁):12,13,14,15,15,15,这组数据中的众数,平均数分别为( )
| A. | 12,14 | B. | 12,15 | C. | 15,14 | D. | 15,13 |
2.在$\sqrt{3}$,$\frac{1}{2}$,0,-2这四个数中,为无理数的是( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
12.下列性质中菱形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 既是轴对称图形又是中心对称图形 |
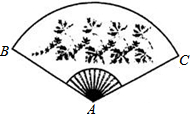 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)