��Ŀ����
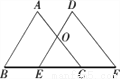
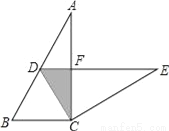
��ͼ����ABC����ƽ�Ƶ���DEFλ�ã����ǵ��ص����ֵ�����ǡ�ABC��һ�룬��BC=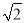 ����BE= ��
����BE= ��
���𰸡�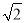 -1.
-1.
���������������֪��OE��AB��
���OEC�ס�ABC��
��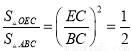 ����
����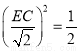 ����ã�EC=1.
����ã�EC=1.
��BE=BC-EC=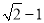 .
.
�����͡������
��������
14
���ε��ܳ�Ϊ16�����ڽǶ����ı�Ϊ1:2�������ε����Ϊ .
8 . ����������ͼ���������֪��������ABCD�У���A+��ADC=180�㣬��A����ADC=1:2��AD=AB=�� ���A=60�㣬 ����D��DE��AB�ڵ�E�����DEA=90�㣬 ���ADE=30�㣬 ��AE=AD=2�� ��DE=, ��S����ABCD=ABDE=.
��ϰ��ϵ�д�
�����Ŀ


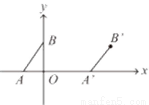
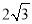 C.
C. 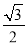 D.
D. 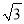
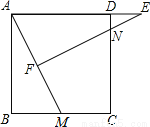
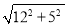 =13��AD=12��
=13��AD=12��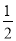 AM=6.5��
AM=6.5��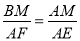 ��
��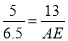 ��
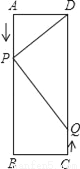
��
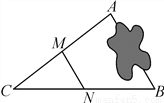
 ABCD�У�EΪ�߶�AD��һ�㣬AE=4ED��CE��BD���ڵ�F����DF=4cm����BF�ij�Ϊ������������
ABCD�У�EΪ�߶�AD��һ�㣬AE=4ED��CE��BD���ڵ�F����DF=4cm����BF�ij�Ϊ������������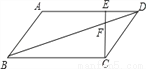
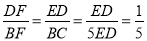 ����
����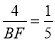 ��
��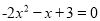 �� ��2��
�� ��2��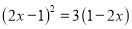 .
.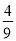 B.
B. 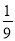 C.
C. 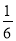 D.
D. 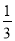
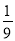 .
.
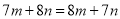 B.
B. 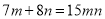
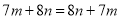 D.
D. 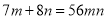
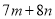 ��һ������
��һ������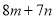 �����Ա�ѡ�����
�����Ա�ѡ�����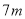 ��
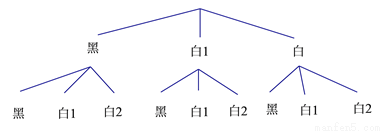
��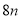 ����ͬ������ܺϲ������Ա�ѡ�����
����ͬ������ܺϲ������Ա�ѡ����� 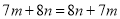 �����Ա�ѡ����ȷ��
�����Ա�ѡ����ȷ��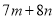 ����
����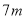 ��
��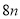 �ĺͣ�������
�ĺͣ�������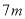 ��
��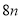 �Ļ������Ա�ѡ�����
�Ļ������Ա�ѡ�����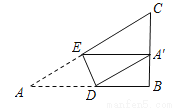
 B.
B. 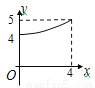
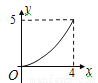 D.
D.