题目内容
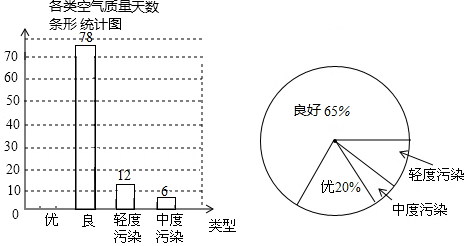
1. 如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是-$\sqrt{10}$+1.
如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是-$\sqrt{10}$+1.
分析 在三角形AOB中,利用勾股定理求出AB的长,即可确定出AP的长,得到P表示的实数.
解答 解:在Rt△AOB中,OA=1,OB=3,
根据勾股定理得:AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴AP=AB=$\sqrt{10}$,
∴OP=AP-OA=$\sqrt{10}$-1,
则P表示的实数为-$\sqrt{10}$+1.
故答案为:-$\sqrt{10}$+1.
点评 此题考查了勾股定理,以及实数与数轴,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
9.下列说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 1是最小的正数 | ||
| C. | 一个有理数不是整数就是分数 | D. | 与0具有相反意义的量是0 |
10.使分式$\frac{2}{{x}^{2}-4}$有意义的x取值范围是( )
| A. | x≠2 | B. | x≠-2 | C. | x≠2且x≠-2 | D. | x≠2或x≠-2 |

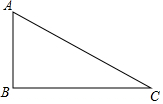 如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.