题目内容
1．若点A（1，m）在反比例函数y=$\frac{3}{x}$的图象上，则m的值为3．分析 直接把点A（1，m）代入函数解析式，即可求出m的值．
解答 解：∵点A（1，m）在反比例函数y=$\frac{3}{x}$的图象上，
∴m=$\frac{3}{1}$=3．
故答案为：3．
点评 本题主要考查点在函数图象上的含义，点在函数图象上，点的坐标一定满足函数解析式．
练习册系列答案
相关题目
12．点P（-1，2）关于y轴的对称点为（ ）
| A． | （1，2） | B． | （-1，-2） | C． | （2，-1） | D． | （1，-2） |
如图，在矩形ABCD中，BF=CE，求证：AE=DF．
6．
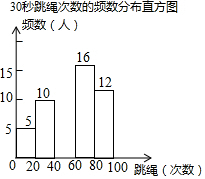某校为迎接体育中考，了解学生的体育情况，学校随机调查了本校九年级50名学生“30秒跳绳”的次数，并将调查所得的数据整理如下：
30秒跳绳次数的频数、频率分布表
根据以上图表信息，解答下列问题：
（1）表中的a=0.2，m=16；
（2）请把频数分布直方图补充完整；（画图后请标注相应的数据）
（3）若该校九年级共有600名学生，请你估计“30秒跳绳”的次数60次以上（含60次）的学生有多少人？
某校为迎接体育中考，了解学生的体育情况，学校随机调查了本校九年级50名学生“30秒跳绳”的次数，并将调查所得的数据整理如下：30秒跳绳次数的频数、频率分布表
| 成绩段 | 频数 | 频率 |
| 0≤x＜20 | 5 | 0.1 |
| 20≤x＜40 | 10 | a |
| 40≤x＜60 | b | 0.14 |
| 60≤x＜80 | m | c |
| 80≤x＜100 | 12 | n |
（1）表中的a=0.2，m=16；
（2）请把频数分布直方图补充完整；（画图后请标注相应的数据）
（3）若该校九年级共有600名学生，请你估计“30秒跳绳”的次数60次以上（含60次）的学生有多少人？
13．
如何求tan75°的值？按下列方法作图可解决问题，如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BN上截取线段BD，使BD=AB，连接AD，依据此图可求得tan75°的值为（ ）
如何求tan75°的值？按下列方法作图可解决问题，如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BN上截取线段BD，使BD=AB，连接AD，依据此图可求得tan75°的值为（ ）| A． | 2$-\sqrt{3}$ | B． | 2+$\sqrt{3}$ | C． | 1+$\sqrt{3}$ | D． | $\sqrt{3}-1$ |
为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=21m，∠BAC=53°，求这颗古杉树AB的长度．