题目内容
17.若抛物线y=$\frac{1}{2}$x2与直线y=x+m只有一个交点,则交点坐标为(1,$\frac{1}{2}$).分析 联立两解析式,消去y可得到一个关于x的一元二次方程,令其判别式为0可求得m的值,再求其交点坐标即可.
解答 解:
联立两解析式可得$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}}\\{y=x+m}\end{array}\right.$,
消去y,整理可得:x2-2x-2m=0,
∵两函数只有一个交点,
∴该一元二次方程有两个相等的实数根,
∴△=0,即4+8m=0,解得m=-$\frac{1}{2}$,
∵方程为x2-2x+1=0,
∴x1=x2=1,代入可求得y=$\frac{1}{2}$,
∴抛物线与直线的交点坐标为(1,$\frac{1}{2}$),
故答案为:(1,$\frac{1}{2}$).
点评 本题主要考查二次函数的性质,掌握函数交点的个数与相应一元二次方程根的个数的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某中学九年级学生共450人,其中男生250人,女生200人.该校对九年级所有学生进行了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
(1)请解释“随机抽取了50名男生和40名女生”的合理性;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校九年级学生体育测试成绩不及格的人数.
| 成绩 | 频数 | 百分比 |
| 不及格 | 9 | 10% |
| 及格 | 18 | 20% |
| 良好 | 36 | 40% |
| 优秀 | 27 | 30% |
| 合计 | 90 | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校九年级学生体育测试成绩不及格的人数.
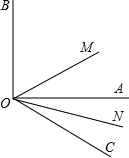 如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.
如图,∠AOB=90°,OM是∠BOC的平分线,ON是∠AOC的平分线,求∠MON的度数.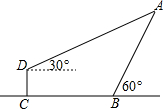 如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)
如图,一水库大坝AB的坡角为60°,在距离B点6米处有一平台CD,在D点测得点A的仰角为30°,已知点A,B,C,D在同一平面上,CD=2米,求这个大坝的高度.(结果保留很号)