��Ŀ����
����Ŀ��С�θ���ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����������С�ε�̽�����̣��벹��������
��ͼ�������ʽ�����̽����������С�ε�̽�����̣��벹��������
��1���±���![]() ��
��![]() �ļ����Ӧֵ
�ļ����Ӧֵ
| ������ | -2 | -1 | 0 | 1 | 2 |
| 3 | ������ |
| ������ | -8 | -3 | 0 | m | n | 1 | 3 | ������ |
��ֱ��д����![]() =�� m=�� n=��
=�� m=�� n=��
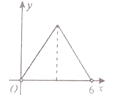
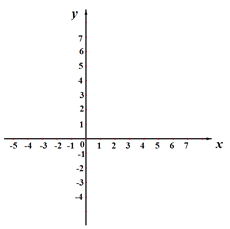
��2����ͼ��С����ƽ��ֱ������ϵ�У�������ϱ����Ѿ������IJ��ֶ�ӦֵΪ����ĵ㣬�����ʣ�µĵ㣬�������ú�����ͼ��
��3����ֱ��д������![]() ��ͼ�����ʣ�����д��һ�����ɣ�
��ͼ�����ʣ�����д��һ�����ɣ�
��4�����ϻ����ĺ���ͼ������⣺������![]() ��������ͬ�Ľ⣬ֱ��д��
��������ͬ�Ľ⣬ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��1��1��0 ��2����ͼ������ ��3���ع���![]() �����𰸲�Ψһ�� ��4��
�����𰸲�Ψһ�� ��4��![]()
��������
��1�����ݴ���ϵ�������![]() ��ֵ���ٴ���
��ֵ���ٴ���![]() ��
��![]() ���������m��n��ֵ��
���������m��n��ֵ��
��2��������㷨����������ͼ�ɣ�
��3�����ݣ�2���к�����ͼ��д������һ�����ʼ��ɣ�
��4������ͼ���ɵú���![]() ��
��![]() ��������ͬ�Ľ��㣬���ݶ��κ�����������⼴�ɣ�
��������ͬ�Ľ��㣬���ݶ��κ�����������⼴�ɣ�
��1����![]() ����
����![]() ��
��
![]()
![]()
���![]()
��![]()
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]() ��
��
��2����ͼ��ʾ��

��3���ع���![]() ��
��
��4����ֱ��![]() ���ɣ�1����
���ɣ�1����![]()
�߷���![]() ��������ͬ�Ľ�
��������ͬ�Ľ�
�ຯ��![]() ��
��![]() ��������ͬ�Ľ���
��������ͬ�Ľ���
����ͼ��֪��������![]() ��������ͬ�Ľ�ʱ��
��������ͬ�Ľ�ʱ��![]()
��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�