题目内容
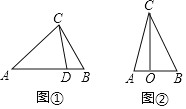
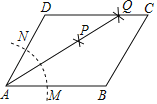
【题目】如图，
是
的边
上一点，
，
交
于点
，若
．
（1）求证：四边形
是平行四边形；
（2）若
，
，求四边形的面积．
【答案】（1）证明见解析；（2）25
．
【解析】
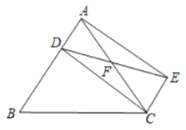
（1）首先利用ASA得出△DAF≌△ECF，进而利用全等三角形的性质得出CE=AD，即可得出四边形ACDE是平行四边形；
（2）由AE⊥EC，四边形ADCE是平行四边形，可推出四边形ADCE是矩形，由F为AC的中点，求出AC，根据勾股定理即可求得AE，由矩形面积公式即可求得结论．
解：（1）证明：∵CE∥AB，
∴∠BAC=∠ECA，
在△DAF和△ECF中，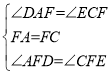
，
∴△DAF≌△ECF（ASA），
∴CE=AD，
∴四边形ADCE是平行四边形；
（2）∵AE⊥EC，四边形ADCE是平行四边形，
∴四边形ADCE是矩形，
在Rt△AEC中，F为AC的中点，
∴AC=2EF=10，
∴AE2=AC2-EC2=102-52=75，
∴AE=5，
∴四边形ADCE的面积=AEEC=25．
练习册系列答案
相关题目
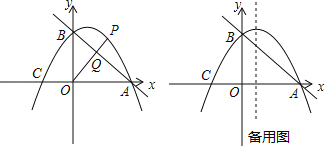
【题目】小涛根据学习函数的经验，对函数
的图像与性质进行了探究，下面是小涛的探究过程，请补充完整：
（1）下表是
与
的几组对应值
| ．．． | -2 | -1 | 0 | 1 | 2 |
| 3 | ．．． |
| ．．． | -8 | -3 | 0 | m | n | 1 | 3 | ．．． |
请直接写出：
=， m=， n=；
（2）如图，小涛在平面直角坐标系中，描出了上表中已经给出的部分对应值为坐标的点，再描出剩下的点，并画出该函数的图象；
（3）请直接写出函数的图像性质：；（写出一条即可）
（4）请结合画出的函数图象，解决问题：若方程
有三个不同的解，直接写出
的取值范围．
