题目内容
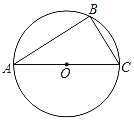
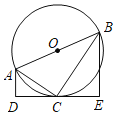
【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=![]() ,CE=3,则
,CE=3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() πC.
πC.![]() πD.
πD.![]() π
π
【答案】D
【解析】
连接OC,由AB是⊙O的直径得到∠ACB=90°,由此证得∠DAC=∠ECB,再证△ADC∽△CEB,列对应边成比例由此求出∠ABC=30°,根据直线DE与⊙O相切于点C求出∠ACD=∠ABC=30°求出AB得到半径,再利用弧长公式计算.
解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,BE⊥DE,
∴∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB,
∴![]() ,即
,即![]() ,
,
∵tan∠ABC=![]() ,
,
∴∠ABC=30°,
∴AB=2AC,∠AOC=60°,
∵直线DE与⊙O相切于点C,
∴∠ACD=∠ABC=30°,
∴AC=2AD=2![]() ,
,
∴AB=4![]() ,
,
∴⊙O的半径为2![]() ,
,
∴![]() 的长为:
的长为:![]() =
=![]() π,
π,
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小涛根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
请直接写出:![]() =, m=, n=;
=, m=, n=;
(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数![]() 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)
(4)请结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,直接写出
有三个不同的解,直接写出![]() 的取值范围.
的取值范围.