题目内容
8.观察下列式子:$\frac{1}{1×2}$=1-$\frac{1}{2}$,
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…
将以上三个等式两边分别相加得:
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$
用你发现是规律解答下列问题:
(1)①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$=$\frac{2015}{2016}$.
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$(其中n为大于1的自然数).
(2)探究并计算:
$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$.
分析 (1)①根据发现的规律进行计算即可;
②根据发现的规律进行计算即可;
(2)首先提取$\frac{1}{4}$,再根据发现的规律进行计算即可.
解答 解:(1)根据题意得:①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$=1-$\frac{1}{2016}$=$\frac{2015}{2016}$;
故答案为:$\frac{2015}{2016}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
故答案为:$\frac{n}{n+1}$;
(2)$\frac{1}{2×4}+\frac{1}{4×6}+\frac{1}{6×8}+$…+$\frac{1}{2014×2016}$=$\frac{1}{4}$($\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$+…+$\frac{1}{1007×1008}$)
=$\frac{1}{4}$×$\frac{1007}{1008}$
=$\frac{1007}{4032}$.
点评 本题考查了有理数的混合运算、数字的变化;根据发现的规律进行计算是解决问题的关键.

练习册系列答案
相关题目
19.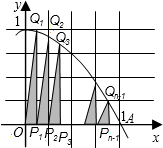 如图,记抛物线y=-x2+1的图象与x正半轴的交点为A,将线段OA分成n等份,设分点分别为P1,P2,…,Pn-1,过每个分点作x轴的垂线,分别与抛物线交于点Q1,Q2,…,Qn-1,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}},{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )
如图,记抛物线y=-x2+1的图象与x正半轴的交点为A,将线段OA分成n等份,设分点分别为P1,P2,…,Pn-1,过每个分点作x轴的垂线,分别与抛物线交于点Q1,Q2,…,Qn-1,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}},{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )
 如图,记抛物线y=-x2+1的图象与x正半轴的交点为A,将线段OA分成n等份,设分点分别为P1,P2,…,Pn-1,过每个分点作x轴的垂线,分别与抛物线交于点Q1,Q2,…,Qn-1,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}},{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )
如图,记抛物线y=-x2+1的图象与x正半轴的交点为A,将线段OA分成n等份,设分点分别为P1,P2,…,Pn-1,过每个分点作x轴的垂线,分别与抛物线交于点Q1,Q2,…,Qn-1,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}},{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.
如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.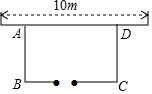 如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门.
如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门.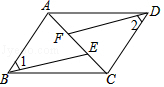 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠1=∠2,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠1=∠2,AF=CE. 如图,△ABC中,点D,E分别在边AB,AC上,∠ADE=∠C,∠BAC的平分线AG分别交线段DE,BC于点F,G.
如图,△ABC中,点D,E分别在边AB,AC上,∠ADE=∠C,∠BAC的平分线AG分别交线段DE,BC于点F,G.