题目内容
 如图,直线y=x向右平移b个单位后得到直线l,l与函数y=
如图,直线y=x向右平移b个单位后得到直线l,l与函数y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:先利用函数图象“左加右减”的平移规律,得出直线l的方程为y=x-b,与反比例函数联立消去y后,得到关于x的方程,整理后得到x2=bx+k,并令直线l方程中y=0,求出x的值,确定出B的坐标,得出OB2,设出A的坐标,利用勾股定理表示出OA2,化简OA2-OB2=2k,由OA2-OB2=8,即可求出k的值.
解答:解:直线y=x向右平移b个单位后得直线l:y=x-b,l与函数y=
(x>0)相交于点A,
∴x-b=
,则x2-bx-k=0.
∴x2=bx+k.
新直线与x轴交于点B(b,0),设点A的坐标为(x,x-b),
∵OA2-OB2=x2+(x-b)2-b2=2x2-2bx=2(bx+k)-2bx=2k,
∴2k=8,
∴k=4.
| k |
| x |
∴x-b=
| k |
| x |
∴x2=bx+k.
新直线与x轴交于点B(b,0),设点A的坐标为(x,x-b),
∵OA2-OB2=x2+(x-b)2-b2=2x2-2bx=2(bx+k)-2bx=2k,
∴2k=8,
∴k=4.
点评:此题考查了反比例函数与一次函数的交点问题,一次函数的平移规律,利用了转化及方程的思想,其中得出y=x平移后直线l的方程是解本题的关键.

练习册系列答案
相关题目
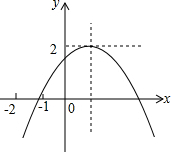 已知二次函数y=ax2+bx+c的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,以下结论:①b2-4ac>0,②abc<0,③m<2,④4a+c>2b中,正确的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,以下结论:①b2-4ac>0,②abc<0,③m<2,④4a+c>2b中,正确的个数是( )| A、1 | B、2 | C、3 | D、4 |
下列命题的逆命题是假命题的是( )
| A、直角三角形中斜边上的中线等于斜边的一半 |
| B、两直线平行,内错角相等 |
| C、等腰三角形的两个底角相等 |
| D、对顶角相等 |
 如图,2×2的正方形网格中,格点O是半径为1的圆的圆心,则图中两个小扇形(阴影部分)的面积之和为
如图,2×2的正方形网格中,格点O是半径为1的圆的圆心,则图中两个小扇形(阴影部分)的面积之和为


