题目内容
4.关于x的不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥4}\\{x<m}\end{array}\right.$有4个整数解,则m的取值范围为8<m≤9.分析 首先解不等式组求得x的范围,根据不等式组有4个整数解即可得到关于m的不等式,从而求解.
解答 解:$\left\{\begin{array}{l}{\frac{x+3}{2}≥4}\\{x<m}\end{array}\right.$,
解$\frac{x+3}{2}≥4$得:x≥5,
则不等式组的解集是:5≤x<m.
∵等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥4}\\{x<m}\end{array}\right.$有4个整数解,
∴8<m≤9.
故答案是:8<m≤9.
点评 本题考查了一元一次不等式组的整数解:解决此类问题的关键在于正确解得不等式组,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件求得不等式组的整数解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9.已知点P(-3,4),则点P到x轴的距离和到y轴的距离分别为( )
| A. | 3,4 | B. | -3,4 | C. | 4,3 | D. | 4,-3 |
14. 已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
 已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
 尺规作图:已知:∠1,利用尺规作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法)
尺规作图:已知:∠1,利用尺规作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法) 如图,?ABCD中,∠B+∠D=144°,则∠D=72°.
如图,?ABCD中,∠B+∠D=144°,则∠D=72°.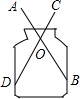 如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.