题目内容
20. 如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )
如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )| A. | 29 | B. | 30 | C. | 31 | D. | 32 |
分析 先证明四边形AECD是平行四边形,得出AE=DC=8,CE=AD,由梯形ABCD的周长即可得出△BCE的周长.
解答 证明:∵AB∥BC,
∴∠A+∠D=180°,∠1+∠AEC=180°,
∵∠1=∠A,
∴∠D=∠AEC,
∴四边形AECD是平行四边形,
∴AE=DC=8,CE=AD,
∵梯形ABCD的周长是45,
∴AD+AB+BC+DC=45,
∴△BCE的周长=CE+BE+BC=45-AE-DC=45-8-8=29;
故选:A.
点评 本题考查了梯形的性质、平行四边形的判定与性质、三角形周长的计算;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.为筹备班级的初中毕业联欢会,班长对全班同学爱吃哪几种水果作民意调查,从而最终决定买什么水果.下列调查数据中最值得关注的是( )
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
11.如图示某几何图形的三视图,侧面积是( )


| A. | 9π | B. | 12π | C. | 15π | D. | 24π |
15. 如图是一个几何体的三视图,则这个几何体的表面积是( )
如图是一个几何体的三视图,则这个几何体的表面积是( )
 如图是一个几何体的三视图,则这个几何体的表面积是( )
如图是一个几何体的三视图,则这个几何体的表面积是( )| A. | 140 | B. | 280 | C. | 180 | D. | 360 |
5.一客轮由A码头顺流沿直线航行至B码头,停留一段时间后再沿原线路返回A码头(客轮往返过程中的静水速度不变),则能大致反应客轮离A码头的距离y(海里)与时间x(小时)之间的函数关系的图象是( )
| A. | 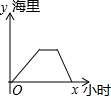 | B. | 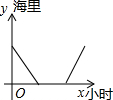 | C. | 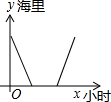 | D. | 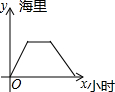 |
9.在$\frac{1}{3}$,0,-1,$\sqrt{2}$这四个实数中,最大的是( )
| A. | $\frac{1}{3}$ | B. | 0 | C. | -1 | D. | $\sqrt{2}$ |
10. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 以上都不正确 |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.