题目内容
12. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.(1)求证:点E是边BC的中点;
(2)当以点O,D,E,C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形;
(3)求证:4DE2=BD•BA.
分析 (1)利用EC为⊙O的切线,ED也为⊙O的切线可求EC=ED,再求得EB=EC,EB=ED可知点E是边BC的中点;
(2)当四边形ODEC为正方形时,∠OCD=45°,由于AC为直径得到∠ADC=90°,于是得到∠A=∠ADC-∠OCD=90°-45°=45°,根据∠ACB=90°,于是得到结论△ABC是等腰直角三角形;
(3)由AC是⊙O是直径,得到CD⊥AB,由于∠ACB=90°,证得△BCD∽△BAC,得到$\frac{BC}{BA}=\frac{BD}{BC}$,即BC2=BD•BA,由(1)可知BC=2DE,即可得到结论.
解答  证明:(1)连接OD,
证明:(1)连接OD,
∵DE为切线,
∴∠EDC+∠ODC=90°,
∵∠ACB=90°,
∴∠ECD+∠OCD=90°,
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴EC=ED,
∵AC为直径,
∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°.
∴∠B=∠BDE,
∴ED=EB.
∴EB=EC,
即点E是边BC的中点,
(2)当四边形ODEC为正方形时,∠OCD=45°,
∵AC为直径∴∠ADC=90°,
∴∠A=∠ADC-∠OCD=90°-45°=45°,
又∵∠ACB=90°,
∴△ABC是等腰直角三角形;
(3)∵AC是⊙O是直径,
∴CD⊥AB,
∵∠ACB=90°,
∴△BCD∽△BAC,
∴$\frac{BC}{BA}=\frac{BD}{BC}$,即BC2=BD•BA,
由(1)可知BC=2DE,
∴4DE2=BD•BA.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
20. 如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )
如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )
 如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )
如图,梯形ABCD中,AB∥BC,∠1=∠A,DC=8,梯形ABCD的周长是45,则△BCE的周长是( )| A. | 29 | B. | 30 | C. | 31 | D. | 32 |
17.已知四边形ABCD的四个顶点的坐标分别为A(-1,0),B(5,0),C(6,2),D(0,2),直线y=kx+2将该四边形分成面积相等的两部分,则k的值为( )
| A. | -$\frac{2}{5}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{2}{7}$ |
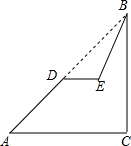 如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号).
如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号).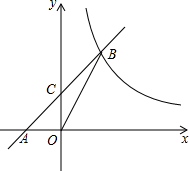 已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.