题目内容
8.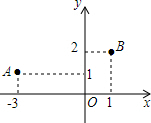 如图,在平面直角坐标系中点A(-3,1),点B(1,2),一束光线从点A处沿直线射出经x轴反射后,正好经过点B,则光线从A到B所经过路程为5.
如图,在平面直角坐标系中点A(-3,1),点B(1,2),一束光线从点A处沿直线射出经x轴反射后,正好经过点B,则光线从A到B所经过路程为5.
分析 利用入射角等于反射角的原理可以△ADC∽△BEC,相似三角形的知识及勾股定理可以求出AC,BC的长,相加即可.
解答 解:由题意得:∠ADC=∠BEC=90°,∠ACD=∠BCE,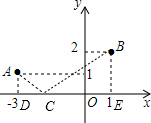
∴△ADC∽△BEC,
∴DC:AD=CE:EB,
DC:1=(4-DC):2
解得DC=$\frac{4}{3}$,
∴CE=$\frac{8}{3}$,
∴AC=$\sqrt{1+\frac{16}{9}}=\frac{5}{3}$,BC=$\frac{10}{3}$,
∴AC+BC=5,
故答案为5
点评 本题考查了相似三角形的判定与性质,坐标与图形变换,点的反射问题;利用相似三角形的性质得到相关结论是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.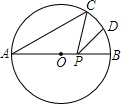 如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )
 如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
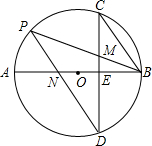 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,