题目内容
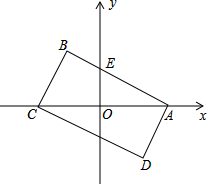矩形ABCD在直角坐标系中的位置如图所示，AB、CD与y轴的交点分别为E、F，点O是矩形对角线的交点，AB=8，BC=6．求矩形顶点A，B，C，D和E，F的坐标．考点：矩形的性质,坐标与图形性质
专题：
分析：根据O是矩形对角线的交点且对角线交点是矩形的中心所以O是对角线AC的中点，且为EF的中点AB=8，BC=6勾股定理可得AC=10由于O是中点，进而利用相似三角形的判定与性质分别得出各点坐标．
解答：
解：∵AB=8，BC=6
∴AC=10，
由于O是中点所以A（5，0），C（-5，0）
∵∠EAO=∠BAC，∠AOE=∠ABC，
∴△AOE∽△ABC
∴
=
，
∴
=
，
∴OE=
，
所以OF=
，
E（0，
），F（0，-
）
过D作DG⊥x轴于点G，
∵∠GCD=∠ACD，∠CGD=∠CDA，
∴△CDG∽△ACD
∴
=
∴
=
，
解得：DG=
，
同理可得：△ADG∽△ACD
=
，
=
，
解得：AG=
，
所以OG=5-
=
，
所以点D（
，-
）
B和D关于原点对称
B（-
，
）
所以A（5，0），B（-
，
），C（-5，0），D（
，-
），E（0，
），F（0，-
）．
解：∵AB=8，BC=6∴AC=10，
由于O是中点所以A（5，0），C（-5，0）
∵∠EAO=∠BAC，∠AOE=∠ABC，
∴△AOE∽△ABC
∴
| EO |
| BC |
| AO |
| AB |
∴
| EO |
| 6 |
| 5 |
| 8 |
∴OE=
| 15 |
| 4 |
所以OF=
| 15 |
| 4 |
E（0，
| 15 |
| 4 |
| 15 |
| 4 |
过D作DG⊥x轴于点G，
∵∠GCD=∠ACD，∠CGD=∠CDA，
∴△CDG∽△ACD
∴
| DG |
| AD |
| CD |
| AC |
∴
| DG |
| 6 |
| 8 |
| 10 |
解得：DG=
| 24 |
| 5 |
同理可得：△ADG∽△ACD
| DG |
| CD |
| AG |
| AD |
| ||
| 8 |
| AG |
| 6 |
解得：AG=
| 18 |
| 5 |
所以OG=5-
| 18 |
| 5 |
| 7 |
| 5 |
所以点D（
| 7 |
| 5 |
| 24 |
| 5 |
B和D关于原点对称
B（-
| 7 |
| 5 |
| 24 |
| 5 |
所以A（5，0），B（-
| 7 |
| 5 |
| 24 |
| 5 |
| 7 |
| 5 |
| 24 |
| 5 |
| 15 |
| 4 |
| 15 |
| 4 |
点评：此题主要考查了矩形的性质以及相似三角形的判定与性质，得出DG，AG的长是解题关键．
练习册系列答案
相关题目
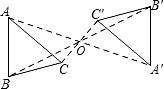如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（ ）| A、点A与点A′是对称点 |
| B、BO=B′O′ |
| C、∠ACB=∠C′A′B′ |
| D、△ABC≌△A′B′C′ |
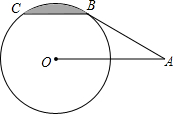已知AB切⊙O于点B，OA=2
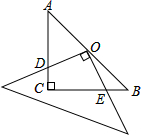如图，在等腰Rt△ABC中，∠C=90°，点O是AB的中点，边AC的长为a，将一块边长足够大的三角板的直角顶点放在O点处，将三角板绕点O旋转，始终保持三角板的直角边与AC相交，交点为点D，另一条直角边与BC相交，交点为点E，证明：等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a．
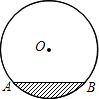如图，是一个圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为32cm，水管半径为20cm，AB为⊙O的劣弧，求截面有水部分的最大深度．