题目内容
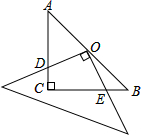 如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为a,将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,证明:等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.
如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为a,将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,证明:等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:连接OC,证得△OCD≌△OBE,得出CD=BE,进一步把CD与CE长度之和转化为等腰Rt△ABC的边长即可.
解答:证明:如图,

连接OC,
∵△ABC是等腰直角三角形,O是AB中点,
∴CO=BB,CO⊥AB,∠ACO=
∠ACB=45°,
即∠ACO=∠B=45°,
∵∠DOC+∠COE=∠BOE+∠COE=90°,
∴∠DOC=∠BOE,
∴△OCD≌△OBE,
∴CD=BE.
∴CE+CD=CE+EB=BC=AC=a,
即等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.

连接OC,
∵△ABC是等腰直角三角形,O是AB中点,
∴CO=BB,CO⊥AB,∠ACO=
| 1 |
| 2 |
即∠ACO=∠B=45°,
∵∠DOC+∠COE=∠BOE+∠COE=90°,
∴∠DOC=∠BOE,
∴△OCD≌△OBE,
∴CD=BE.
∴CE+CD=CE+EB=BC=AC=a,
即等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.
点评:本题考查了等腰三角形的性质与判定,全等三角形的判定与性质,等角的余角相等等知识点,结合图形,灵活解决问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
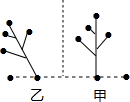 如图,乙图案变为甲图案,需要用到( )
如图,乙图案变为甲图案,需要用到( )| A、旋转、对称 |
| B、平移、对称 |
| C、旋转、平移 |
| D、旋转、旋转 |
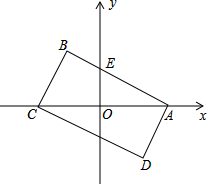 矩形ABCD在直角坐标系中的位置如图所示,AB、CD与y轴的交点分别为E、F,点O是矩形对角线的交点,AB=8,BC=6.求矩形顶点A,B,C,D和E,F的坐标.
矩形ABCD在直角坐标系中的位置如图所示,AB、CD与y轴的交点分别为E、F,点O是矩形对角线的交点,AB=8,BC=6.求矩形顶点A,B,C,D和E,F的坐标. 已知:抛物线y=x2-4x+3与y轴的交点的坐标是(0,3).求:
已知:抛物线y=x2-4x+3与y轴的交点的坐标是(0,3).求: 如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为
如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为 如图:D、E是三角形ABC的边BC上的两点,且BD=DE=AD=AE=EC,则∠BAC的大小等于
如图:D、E是三角形ABC的边BC上的两点,且BD=DE=AD=AE=EC,则∠BAC的大小等于