题目内容
正六边形ABCDEF的边长为2，则对角线AE的长为 ．
考点：正多边形和圆
专题：
分析：根据题意画出图形，过点F作FG⊥AE于点G，先根据正六边形的性质得出∠AFE的度数，再由AF=EF可知FG是AE的垂直平分线，∠GAF=30°，根据锐角三角函数的定义即可得出AG的长，进而得出结论．
解答：
解：如图所示，
过点F作FG⊥AE于点G，
∵多边形ABCDEF是正六边形，
∴∠AFE=120°，AF=EF，
∴FG是AE的垂直平分线，∠GAF=30°，
∴AG=AF•cos30°=2×
=
，
∴AE=2AG=2
．
故答案为：2
．
解：如图所示，过点F作FG⊥AE于点G，
∵多边形ABCDEF是正六边形，
∴∠AFE=120°，AF=EF，
∴FG是AE的垂直平分线，∠GAF=30°，
∴AG=AF•cos30°=2×
| ||
| 2 |
| 3 |
∴AE=2AG=2
| 3 |
故答案为：2
| 3 |
点评：本题考查的是正多边形和圆，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
相关题目
如图，△ABC内接于半圆，AB为直径，设D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．
如图，乙图案变为甲图案，需要用到（ ）| A、旋转、对称 |
| B、平移、对称 |
| C、旋转、平移 |
| D、旋转、旋转 |
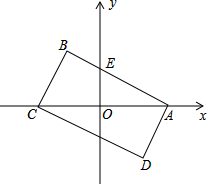矩形ABCD在直角坐标系中的位置如图所示，AB、CD与y轴的交点分别为E、F，点O是矩形对角线的交点，AB=8，BC=6．求矩形顶点A，B，C，D和E，F的坐标．
如图，∠AOB=30°，P是∠AOB内的一点，且OP=4cm，C、D分别是P关于OA、OB的对称点，连结CD、PM、PN，则△PMN的周长为