题目内容
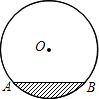如图，是一个圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为32cm，水管半径为20cm，AB为⊙O的劣弧，求截面有水部分的最大深度．考点：垂径定理的应用,勾股定理
专题：
分析：连接OA，过点O作OC⊥AB交AB于点D，先根据垂径定理求出AD的长，再由勾股定理求出OD的长，由CD=OC-OD即可得出结论．
解答：
解：连接OA，过点O作OC⊥AB交AB于点D，
∵水管半径为20cm，其中水面AB宽为32cm，
∴OA=OC=20cm，AD=
AB=16cm，∴OD=
=12cm，
∴CD=OC-OD=20-12=8cm．
所以截面有水部分的最大深度为8cm．
解：连接OA，过点O作OC⊥AB交AB于点D，∵水管半径为20cm，其中水面AB宽为32cm，
∴OA=OC=20cm，AD=
| 1 |
| 2 |
| OA2-AD2 |
∴CD=OC-OD=20-12=8cm．
所以截面有水部分的最大深度为8cm．
点评：本题考查的是垂径定理在实际生活中的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
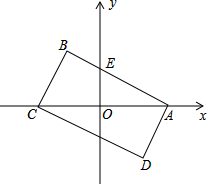矩形ABCD在直角坐标系中的位置如图所示，AB、CD与y轴的交点分别为E、F，点O是矩形对角线的交点，AB=8，BC=6．求矩形顶点A，B，C，D和E，F的坐标．
如图，∠AOB=30°，P是∠AOB内的一点，且OP=4cm，C、D分别是P关于OA、OB的对称点，连结CD、PM、PN，则△PMN的周长为
如图，在△ABC中，∠A=30°，∠B=45°，AB=4，求△ABC的面积．
如图，在直角梯形ABCD中，AD∥BC，AD=1，BC=9，M为AB的中点，以CD为直径画圆P．
如图：D、E是三角形ABC的边BC上的两点，且BD=DE=AD=AE=EC，则∠BAC的大小等于在2，3.5，4，
，-2.3几个有理数中，分数共有（ ）个．
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
若点A（-2，y1）、B（-1，y2）、C（9，y3）是二次函数y=-
x2+3x+
图象上的三点，则y1、y2和y3的大小关系是（ ）
| 1 |
| 2 |
| 5 |
| 2 |
| A、y1＜y2＜y3 |
| B、y1＞y2＞y3 |
| C、y3＞y1＞y2 |
| D、y3＜y1＜y2 |