题目内容
圆内接四边形ABCD中，∠A：∠B：∠C=1：2：4，则∠D= 度．
考点：圆内接四边形的性质
专题：
分析：设∠A=x，则∠B=2x，∠C=4x，再由圆内接四边形的对角互补求出x的值，进而可得出结论．
解答：解：∵圆内接四边形ABCD中，∠A：∠B：∠C=1：2：4，
∴设∠A=x，则∠B=2x，∠C=4x．
∵∠A+∠C=180°，即x+4x=180°，解得x=36°，
∴∠B=2x=72°，
∴∠D=180°-72°=108°．
故答案为：108．
∴设∠A=x，则∠B=2x，∠C=4x．
∵∠A+∠C=180°，即x+4x=180°，解得x=36°，
∴∠B=2x=72°，
∴∠D=180°-72°=108°．
故答案为：108．
点评：本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列等式的变形错误的是（ ）
| A、由a=b得a+5=b+5 | ||||
B、由a=b得
| ||||
| C、由x+2=y+2得x=y | ||||
| D、由-3x=-3y得x=-y |
在Rt△ABC中，∠C=90°，周长为60，斜边与一条直角边之比为13：5，则这个三角形三边长分别是（ ）
| A、25、23、12 |
| B、13、12、5 |
| C、10、8、6 |
| D、26、24、10 |
如图，点D在△ABC的边AC上，添加下列一个条件仍不能判断△ADB与△ABC相似的是（ ）| A、∠ABD=∠C |
| B、∠ADB=∠ABC |
| C、BC2=CD•AC |
| D、AB2=AD•AC |
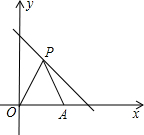如图，在平面直角坐标系中，点P（x，y）是第一象限直线y=-x+6的点，点A（4，0），O是坐标原点，△PAO的面积为S．