题目内容
7.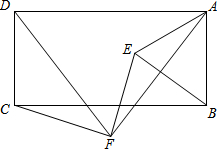 如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
分析 如图,要证明△ABE为等边三角形,只要证明AE=AB,∠EAB=60°即可;为此,首先证明△ADF为等边三角形,求出∠EAF、∠BAF的度数,进而求出∠BAE=60°;由旋转变换的性质、矩形的性质证明AE=AB,即可解决问题.
解答  解:△ABE为等边三角形;证明如下:如图,
解:△ABE为等边三角形;证明如下:如图,
∵四边形ABCD为矩形,
∴AB=DC,∠CDA=∠DAB=90°;
由旋转变换的性质知:
DF=AF,∠DFA=60°,AE=CD,∠EAF=∠CDF,
∴△ADF为等边三角形,AE=AB,
∴∠FDA=∠FAD=60°,
∴∠CDF=∠BAF=30°,∠EAF=∠CDF=30°,
∴∠EAB=60°,而EA=EB,
∴△ABE为等边三角形.
点评 该题以矩形为载体,主要考查了矩形的性质、旋转变换的性质及其应用问题;解题的关键是深入观察图形,准确找出图形中隐含的相等或全等关系.

练习册系列答案
相关题目
 如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC.
如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC. 如图,水泥在传送带上移动的过程可以看做平移 变换.
如图,水泥在传送带上移动的过程可以看做平移 变换.