Question

4．已知二次函数y=ax²+bx+c顶点x轴上，且过A（1，0），B（0，-2）两点．
（1）求二次函数关系式；
（2）若直线y=-2与二次函数交于B，C两点，求△ABC面积；
（3）在抛物线上是否存在P点，使△APC面积与△ABC的面积相等，若存在求P点坐标若不存在，说明理由．

Answer 1

分析 （1）由二次函数y=ax²+bx+c顶点x轴上，得到b²-4ac=0，再把A、B两点代入抛物线解析式，列方程组即可解决问题．
（2）列方程组求出B、C坐标即可解决问题．
（3）存在．如图3中，过点B作BP∥AC交抛物线于P，点P就是满足条件的点，求出直线BP的解析式，列方程组求出点P坐标即可．

解答 解：（1）由题意$\left\{\begin{array}{l}{{b}^{2}-4ac=0}\\{a+b+c=0}\\{c=-2}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-2}\\{b=4}\\{c=-2}\end{array}\right.$，
∴二次函数的解析式为y=-2x²+4x-2．

（2）由$\left\{\begin{array}{l}{y=-2}\\{y=-2{x}^{2}+4x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$，
不妨设B（0，-2），C（2，-2），如图1中，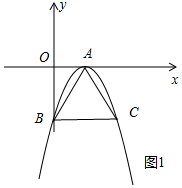

∵B、C两点纵坐标相同，
∴BC∥x轴，
∴S_△ABC=$\frac{1}{2}$×2×2=2．

（3）存在．如图3中，过点B作BP∥AC交抛物线于P．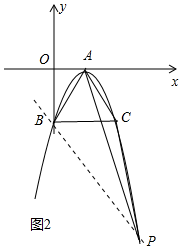

∵PB∥AC，
∴S_△PAC=S_△ABC．
设直线AC解析式为y=kx+b，则有$\left\{\begin{array}{l}{k+b=0}\\{2k+b=-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$，
∴直线AC解析式为y=-2x+2，
则直线PB的解析式为y=-2x-2，
由$\left\{\begin{array}{l}{y=-2x-2}\\{y=-2{x}^{2}+4x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-8}\end{array}\right.$，
∵点B坐标（0，-2），∴点P坐标为（3，-8）．

点评 本题考查二次函数综合题、待定系数法、平行线的性质、两直线平行k相同等知识，解题的关键是灵活运用这些知识解决问题，学会利用平行线的性质构造面积相等的三角形，属于中考常考题型．