题目内容
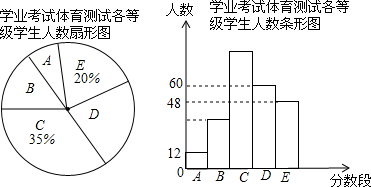
17.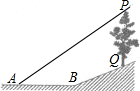 已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.
已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.
分析 在直角三角形QBC中,根据坡度为i=5:12和勾股定理求出QC和BC,从而得出AC,再由直角三角形和tanα=0.75求出PC,继而求出香樟树PQ的高度.
解答  解:如图,PQ⊥AB于点C.
解:如图,PQ⊥AB于点C.
∵在Rt△QBC中,QC:BC=5:12,
∴设QC=5x米,BC=12x米,
∵BQ=13米,
∴(5x)2+(12x)2=132,
∴x=±1(负值舍去),
∴QC=5米,BC=12米.
∵AB=8米,
∴AC=AB+BC=20米.
∵tanα=0.75,
∴$\frac{PC}{AC}$=0.75,
即$\frac{PC}{20}$=0.75,
∴PC=15.
∴PQ=PC-QC=15-5=10米.
故香樟树PQ的高度为10米.
点评 此题考查了解直角三角形的应用-坡度坡角问题,解直角三角形的应用-仰角俯角问题,勾股定理,锐角三角函数的定义,关键是构造两直角三角形根据勾股定理和三角函数求解.

练习册系列答案
相关题目
8.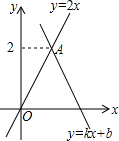 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
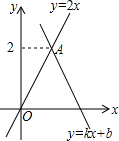 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | x>0 | B. | 0<x<1 | C. | 1<x<2 | D. | x>2 |
2.已知x1、x2是方程x2-5x-6=0的两个根,则代数式x1•x2-x1-x2的值是( )
| A. | 11 | B. | -1 | C. | -11 | D. | 1 |
9.某销售公司为了提高员工的工作积极性,对员工的工资结构进行改革,改革后月工资由基本保障工资与计件奖励工资组成.(计件奖励工资=销售每件的奖励金额×销售的件数)下表是甲、乙两位职工今年三月份的工资情况信息:
求员工的月基本保障工资和销售每件产品的奖励金额各多少元?
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 100 | 80 |
| 月工资(元) | 4500 | 4100 |

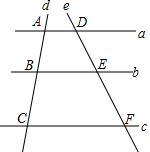 如图,已知直线a∥b∥c,直线d分别于直线a、b、c相交于点A、B、C,直线e分别与直线a、b、c相交于点D、E、F.若AB=2,BC=3,DE=3,则DF的长为$\frac{15}{2}$.
如图,已知直线a∥b∥c,直线d分别于直线a、b、c相交于点A、B、C,直线e分别与直线a、b、c相交于点D、E、F.若AB=2,BC=3,DE=3,则DF的长为$\frac{15}{2}$.