Question

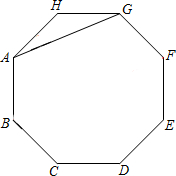如图，AG是正八边形ABCDEFGH的一条对角线．
（1）在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；
（2）两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．

Answer 1

考点：正多边形和圆,全等三角形的判定与性质,正方形的判定

专题：

分析：（1）利用已知得出正八边形，它的内角都为135°，再利用正八边形ABCDEFGH关于直线BF对称，得出∠2+∠3=180°，进而得出答案；
（2）根据题意得出△PAH≌△QCB≌△MDE，则PA=QB=QC=MD．即PQ=QM，故四边形PQMN是正方形，进而求出PQ的长即可得出答案．

解答：解：（1）连接BF，则有BF∥AG．
理由如下：
∵ABCDEFGH是正八边形，
∴它的内角都为135°．
又∵HA=HG，
∴∠1=22.5°，
从而∠2=135°-∠1=112.5°．
由于正八边形ABCDEFGH关于直线BF对称，
∴∠3=

1

2

×135°=67.5°
即∠2+∠3=180°，故BF∥AG．

（2）根据题设可知∠PHA=∠PAH=45°，
∴∠P=90°，同理可得∠Q=∠M=90°，
∴四边形PQMN是矩形．
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°，AH=BC=DE，
∴△PAH≌△QCB≌△MDE，
∴PA=QB=QC=MD．即PQ=QM，
故四边形PQMN是正方形．
在Rt△PAB中，∵∠PAH=45°，AB=2，
∴PA=AB•sin45°=2×

2

2

=

2

，
∴PQ=PA+AB+BQ=

2

+2+

2

=2

2

+2．
故S四边形PQMN=(2

2

+2)2=12+8

2

．

点评：此题主要考查了正多边形和圆以及全等三角形的判定与性质等知识，得出PQ的长是解题关键．