题目内容
 根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.(1)计算AB的长度.
(2)通过计算判断此车是否超速.
考点:解直角三角形的应用
专题:应用题
分析:(1)已知MN=30m,∠AMN=60°,∠BMN=45°求AB的长度,可以转化为解直角三角形;
(2)求得从A到B的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.
(2)求得从A到B的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.
解答:解:(1)在Rt△AMN中,MN=30,∠AMN=60°,
∴AN=MN•tan∠AMN=30
.
在Rt△BMN中,
∵∠BMN=45°,
∴BN=MN=30.
∴AB=AN+BN=(30+30
)米;
(2)∵此车从A点行驶到B点所用时间为6秒,
∴此车的速度为:(30+30
)÷6=5+5
≈13.66,
∵60千米/时≈16.66米/秒,
∴13.66<16.66
∴不会超速.
∴AN=MN•tan∠AMN=30
| 3 |
在Rt△BMN中,
∵∠BMN=45°,
∴BN=MN=30.
∴AB=AN+BN=(30+30
| 3 |
(2)∵此车从A点行驶到B点所用时间为6秒,
∴此车的速度为:(30+30
| 3 |
| 3 |
∵60千米/时≈16.66米/秒,
∴13.66<16.66
∴不会超速.
点评:本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,是MH370五张黑体字符图片.
如图,是MH370五张黑体字符图片.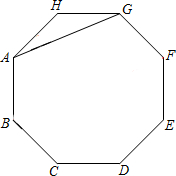 如图,AG是正八边形ABCDEFGH的一条对角线.
如图,AG是正八边形ABCDEFGH的一条对角线. 为了了解八年级800名学生寒假的读书情况,数学小组随机调查了50名八年级学生,并将统计数据制成了扇形统计图如图,其中读1册的有13人,则该校八年级学生中读书册数为3册的约有
为了了解八年级800名学生寒假的读书情况,数学小组随机调查了50名八年级学生,并将统计数据制成了扇形统计图如图,其中读1册的有13人,则该校八年级学生中读书册数为3册的约有 如图,在⊙O中,弦AB=3,半径OA=
如图,在⊙O中,弦AB=3,半径OA=