题目内容
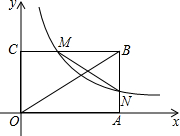 如图,点A在x轴正半轴上,点C在y正半轴上,四边形OABC为矩形,面积为6,双曲线y=
如图,点A在x轴正半轴上,点C在y正半轴上,四边形OABC为矩形,面积为6,双曲线y=| k |
| x |
考点:反比例函数综合题
专题:
分析:设点A的横坐标为a,根据矩形的面积表示出OC,再根据反比例函数图象上的点的坐标特征表示出AN、CM,然后求出BM、BN,再利用勾股定理列式求出OB2、MN2,然后根据2OB=3MN列出关于a、k的方程,求解得到k的值再根据矩形的面积判断出k的取值范围,从而得解.
解答:解:设点A的横坐标为a,则OA=a,
∵矩形OABC的面积为6,
∴OC=
,
∴AN=
,
∵点M在BC上,
∴
=
,
解得:x=
,
∴CM=
,
∴BM=BC-CM=a-
,
BN=AB-AN=
-
,
由勾股定理得,OB2=OA2+AB2=a2+(
)2=
(a4+36),
MN2=BM2+BN2=(a-
)2+(
-
)2=
(6-k)2+
(6-k)2=
(6-k)2•
(a4+36),
∵2OB=3MN,
∴4OB2=9MN2,
∴4×
(a4+36)=9×
(6-k)2•
(a4+36),
∴(6-k)2=16,
解得k1=2,k2=10,
∵矩形OABC的面积为6,点B在双曲线上方,
∴k<6,
∴k的值为2.
故答案为:2.
∵矩形OABC的面积为6,
∴OC=
| 6 |
| a |
∴AN=
| k |
| a |
∵点M在BC上,
∴
| k |
| x |
| 6 |
| a |
解得:x=
| ka |
| 6 |
∴CM=
| ka |
| 6 |
∴BM=BC-CM=a-
| ka |
| 6 |
BN=AB-AN=
| 6 |
| a |
| k |
| a |
由勾股定理得,OB2=OA2+AB2=a2+(
| 6 |
| a |
| 1 |
| a2 |
MN2=BM2+BN2=(a-
| ka |
| 6 |
| 6 |
| a |
| k |
| a |
| a2 |
| 36 |
| 1 |
| a2 |
| 1 |
| 36 |
| 1 |
| a2 |
∵2OB=3MN,
∴4OB2=9MN2,
∴4×
| 1 |
| a2 |
| 1 |
| 36 |
| 1 |
| a2 |
∴(6-k)2=16,
解得k1=2,k2=10,
∵矩形OABC的面积为6,点B在双曲线上方,
∴k<6,
∴k的值为2.
故答案为:2.
点评:本题考查了矩形的性质,反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,利用勾股定理列式表示出OB2、MN2,然后得到关于k飞方程是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
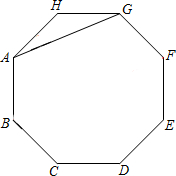 如图,AG是正八边形ABCDEFGH的一条对角线.
如图,AG是正八边形ABCDEFGH的一条对角线.