题目内容
PA、PB是⊙O的切线,A、B是切点,∠APB=80°,点C是圆上异于A、B的任意一点,那么∠ACB= .
考点:切线的性质
专题:
分析:此题注意要分情况讨论:C点在劣弧AB上或点C点在优弧AB上.连接过切点的半径,发现四边形,根据四边形的内角和定理求得∠AOB的度数,进一步根据圆周角定理进行计算即可.
解答:解:连接OA、OB,在AB弧上任取一点C;
∵PA、PB是⊙O的切线,A、B为切点,
连接AC、BC,
∴∠OAP=∠OBP=90°,
∵∠APB=80°,
在四边形OAPB中,可得∠AOB=100°;
则有①若C点在劣弧AB上,则∠ACB=130°;
②若C点在优弧AB上,则∠ACB=50°,
故答案为:130°或50°.

∵PA、PB是⊙O的切线,A、B为切点,
连接AC、BC,
∴∠OAP=∠OBP=90°,
∵∠APB=80°,
在四边形OAPB中,可得∠AOB=100°;
则有①若C点在劣弧AB上,则∠ACB=130°;
②若C点在优弧AB上,则∠ACB=50°,
故答案为:130°或50°.
点评:此题主要考查圆的切线的性质、四边形的内角和、同弧所对的圆心角与圆周角的关系等知识,题目比较典型,难度适中,用了分类讨论思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
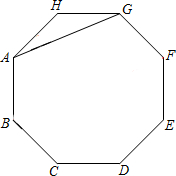 如图,AG是正八边形ABCDEFGH的一条对角线.
如图,AG是正八边形ABCDEFGH的一条对角线. 如图,AB是⊙O的直径,点C、D都在⊙O上,若∠C=20°,则∠ABD的度数等于
如图,AB是⊙O的直径,点C、D都在⊙O上,若∠C=20°,则∠ABD的度数等于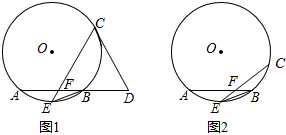 如图1,在⊙O中,E是
如图1,在⊙O中,E是