题目内容
1.若一元二次方程x2-ax+3=0有两个实数根,则a的值可以是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据判别式的意义得到△=(-a)2-4×1×3≥0,即a2≥12,然后对各选项进行判断.
解答 解:根据题意得△=(-a)2-4×1×3≥0,
即a2≥12,
当a=4时满足a2≥12.
故选D.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
16.小新家今年4月份头6天用米量如表:估计小新家4月份用米量为25kg.
| 用米量(kg) | 0.6 | 0.8 | 0.9 | 1.0 |
| 天数 | 1 | 2 | 2 | 1 |
10.下列结论正确的是( )
| A. | 经过圆心的直线是圆的对称轴 | B. | 直径是圆的对称轴 | ||
| C. | 与圆相交的直线是圆的对称轴 | D. | 与直径相交的直线是圆的对称轴 |
11.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为( )
| A. | 6cm | B. | 12cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{6}$cm |
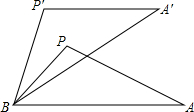 如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$)
如图,△APB绕点B按逆时针方向旋转30°后,得到△A′P′B,且AB=4,那么AA′的长为2$\sqrt{6}$-2$\sqrt{2}$.(不取近似值,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$) 如图,如果∠B=∠C,那么△BAE∽△CAD,△BOD∽△COE.
如图,如果∠B=∠C,那么△BAE∽△CAD,△BOD∽△COE.