题目内容
1.(1)计算:|-2|+($\frac{1}{3}$)-1-($\sqrt{3}$-2010)0-$\sqrt{3}$•tan60°(2)先化简先化简,再求值:$\frac{1+x}{1-x}$÷(x-$\frac{2x}{1-x}$),其中x=$\sqrt{2}$.
分析 (1)根据零指数幂、负整数指数幂的意义和特殊角的三角函数值计算;
(2)先把括号内通分,再把分子因式分解,然后把除法运算化为乘法运算后约分得原式=-$\frac{1}{x}$,最后把x的值代入计算即可.
解答 解:(1)原式=2+3-1-$\sqrt{3}$•$\sqrt{3}$
=2+3-1-3
=1;
(2)原式=$\frac{1+x}{1-x}$÷$\frac{x(1-x)-2x}{1-x}$
=$\frac{1+x}{1-x}$•$\frac{1-x}{-x(1+x)}$
=-$\frac{1}{x}$,
当x=$\sqrt{2}$时,原式=-$\frac{1}{\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
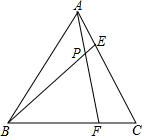 如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.
如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.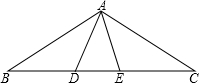 如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..
如图,在△ABC中,AD=AE,BD=CE,∠ADB=∠AEC,那么△ABD≌△ACE,△ABE≌ACD..
 如图,AB=AD=4cm,BC=CD,若∠ABD=60°,则BE=2cm.
如图,AB=AD=4cm,BC=CD,若∠ABD=60°,则BE=2cm.