题目内容
 如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么?
如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么?考点:相似三角形的判定
专题:
分析:由条件可先证得△AEC∽△ADB,可得
=
,则有
=
,且∠EAD=∠CAB,可证得△ADE∽△ABC.
| AE |
| AD |
| AC |
| AB |
| AE |
| AC |
| AD |
| AB |
解答:解:相似,理由如下:
∵BD、CE是△ABC的高,
∴∠ABD+∠A=∠ACE+∠A=90°,
∴∠ABD=∠ACE,且∠A=∠A,
∴△AEC∽△ADB,
∴
=
,即
=
,且∠EAD=∠CAB,
∴△ADE∽△ABC.
∵BD、CE是△ABC的高,
∴∠ABD+∠A=∠ACE+∠A=90°,
∴∠ABD=∠ACE,且∠A=∠A,
∴△AEC∽△ADB,
∴
| AE |
| AD |
| AC |
| AB |
| AE |
| AC |
| AD |
| AB |
∴△ADE∽△ABC.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定是解题的关键,注意用相似找条件.

练习册系列答案
相关题目
2013年12月15日,“玉兔号”月球车月面软着陆后离地球380000千米,能够看到地球等离子层的全貌.380000千米用科学记数法表示为( )
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
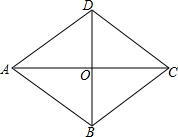 如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为
如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为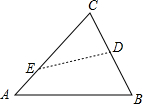 如图,点D在BC上,AC=15cm,BC=9cm,CD=3cm,一动点E在边AC上以1cm/s的速度自点A向点C移动,几秒后△ECD与△ABC相似?
如图,点D在BC上,AC=15cm,BC=9cm,CD=3cm,一动点E在边AC上以1cm/s的速度自点A向点C移动,几秒后△ECD与△ABC相似? 如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.
如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.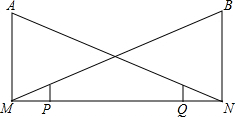 如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.
如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.