题目内容
 如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )
如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )| A、45° | B、55° |
| C、60° | D、75° |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形性质得出∠ABD=∠C=60°,AB=BC,证出△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,根据三角形外角性质得出∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC,即可得出答案.
解答:解:∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
故选C.
∴∠ABD=∠C=60°,AB=BC,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
故选C.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形外角性质的应用,解此题的关键是求出△ABD≌△BCE.

练习册系列答案
相关题目
一边长为4的等腰三角形周长为18,则其腰长为( )
| A、4 | B、7 | C、4或7 | D、10 |
 已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.
已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.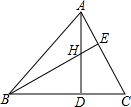 如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.
如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.